Kendra Leota's Calculus Questions @ Yahoo Answers

[MarkFL]

Here are the questions:

Calculus word problems?

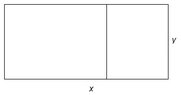
1. A rancher has 200 ft of fencing with which to enclose two adjacent rectangular corrals, as shown. What dimensions should be used so that the enclosed area will be a maximum?

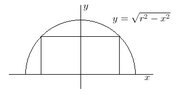
2.A rectangle is inscribed inside a semi-circle with intercepts at (-8,0), (0,8), and (8,0). Find a function that models the area of the rectangle in terms of half of the base, x, of the rectangle, as shown in the figure below. Determine what x-value will produce an area of 30 square units.

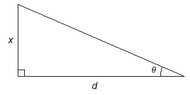
3. A camera is mounted at a point 300 ft from the base of a rocket launching pad. The rocket rises vertically when launched. Express the distance, x, traveled by the rocket as a function of the camera elevation angle, theta. Find the distance traveled by the rocket when the angle of elevation is 20 degrees.

PLEASE EXPLAIN

I have posted a link there to this topic so the OP can see my work.

 

[MarkFL]

Hello Kendra Leota,

1.) I would first draw a sketch of the corrals:

View attachment 1204

We can now see that we have the objective function (the enclosed area $A$):

\(\displaystyle A(x,y)=xy\)

subject to the constraint (the amount of fencing $F$):

\(\displaystyle 2x+3y=F\)

I know of 3 methods to use here. The first two will require that we express $A$ as a function of 1 variable, so if we solve the constraint for $y$, we find:

\(\displaystyle y=\frac{F-2x}{3}\)

and by substitution we now have:

\(\displaystyle A(x)=x\left(\frac{F-2x}{3} \right)=\frac{1}{3}\left(x(F-2x) \right)\)

i) Pre-calculus technique:

We see that we have a parabolic function opening down, and so the vertex will be the global maximum. The vertex must be midway between the roots, and we can see the roots are at:

\(\displaystyle x=0,\,\frac{F}{2}\)

and so the axis of symmetry, which contains the vertex, is the line:

\(\displaystyle x=\frac{F}{4}\)

and thus:

\(\displaystyle y=\frac{F-2\left(\frac{F}{4} \right)}{3}=\frac{F}{6}\)

We then see that half of the fencing is in the horizontal segments and half is in the vertical segments.

ii) Using differentiation

Let's write the area function as:

\(\displaystyle A(x)=\frac{1}{3}\left(Fx-2x^2 \right)\)

Now, equate the first derivative to zero to find the critical point:

\(\displaystyle A'(x)=\frac{F}{3}-\frac{4}{3}x=0\implies x=\frac{F}{4}\)

$y$ is found in the same way as the first method. We see that:

\(\displaystyle A''(x)=-\frac{4}{3}<0\)

and so we know the function is concave down everywhere, so our critical value is a maximum.

iii) Multi-variable technique (Lagrange multipliers):

We obtain the following system:

\(\displaystyle y=2\lambda\)

\(\displaystyle x=3\lambda\)

This implies:

\(\displaystyle 2x=3y\)

and putting this into the constraint, we find:

\(\displaystyle x=\frac{F}{4},\,y=\frac{F}{6}\)

To finish up, letting \(\displaystyle F=200\text{ ft}\), we find the dimensions which maximize the enclosed area is:

\(\displaystyle x=50\text{ ft}\)

\(\displaystyle y=\frac{100}{3}\text{ ft}\)

2.) Let's draw a sketch:

View attachment 1205

We can see that we have the area of the rectangle as:

\(\displaystyle A(x,y)=2xy\)

Using the fact that $y$ is a function of $x$, we find:

\(\displaystyle A(x)=2x\sqrt{r^2-x^2}\)

Using the given \(\displaystyle r=8\), we have:

\(\displaystyle A(x)=2x\sqrt{8^2-x^2}\)

To find the value of $x$ when $A=30$, we may write:

\(\displaystyle 30=2x\sqrt{8^2-x^2}\)

Square both sides:

\(\displaystyle 900=4x^2\left(64-x^2 \right)\)

\(\displaystyle 225=x^2\left(64-x^2 \right)=64x^2-x^4\)

\(\displaystyle x^4-64x^2+225=0\)

Observing that we have a quadratic in $x^2$, we may apply the quadratic formula to obtain:

\(\displaystyle x^2=\frac{64\pm\sqrt{(-64)^2-4(1)(225)}}{2(1)}=32\pm\sqrt{799}\)

Hence, taking the positive root as we require $0\le x\le8$):

\(\displaystyle x=\sqrt{32\pm\sqrt{799}}\)

3.) Again, let's draw a sketch:

View attachment 1206

We now see that we may relate the two known sides of the triangle to the angle using the tangent function:

\(\displaystyle \tan(\theta)=\frac{x}{d}\implies x=d\tan(\theta)\)

Using the given \(\displaystyle d=300\text{ ft}\) we have:

\(\displaystyle x(\theta)=300\tan(\theta)\text{ ft}\)

To find the distance traveled by the rocket when $\theta=20^{\circ}$, we may write:

\(\displaystyle x\left(20^{\circ} \right)=300\tan\left(20^{\circ} \right)\text{ ft}\approx109.191070279861\text{ ft}\)