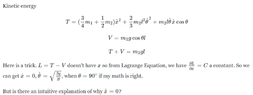Latex Troubleshooting: My Attempted Solution
- Context: LaTeX
- Thread starter mattlfang
- Start date
-
- Tags
- Latex Troubleshooting
Click For Summary
Discussion Overview
The discussion revolves around troubleshooting LaTeX formatting issues and exploring the dynamics of a wheel and stick system, particularly focusing on the implications of rolling without slipping and the conservation of momentum in the presence of friction. The scope includes conceptual clarification and technical reasoning related to physics principles.
Discussion Character
- Technical explanation
- Conceptual clarification
- Debate/contested
Main Points Raised
- Some participants express difficulty in getting LaTeX to work correctly, suggesting the use of double brackets for expressions.
- There is a discussion about the initial conditions of the center of mass of the wheel and stick system, questioning the forces acting on it and the implications for momentum conservation.
- One participant proposes a model involving a wheel on rails with a gap for the stick to swing, questioning the motion of the system without energy loss.
- Another participant seeks clarification on the proposed model, expressing confusion about the physical setup and its implications for momentum conservation when friction is present.
- Participants discuss the concept of "rolling without slipping," noting that it implies the point of contact is at rest relative to the surface, and that friction cannot be ignored in this context.
- There is a suggestion that the wheel-on-rails setup differs from a pendulum model, prompting further exploration of the dynamics when the stick swings through a full 360°.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the implications of rolling without slipping in relation to momentum conservation, with multiple competing views remaining on how friction interacts with these concepts.
Contextual Notes
Participants express uncertainty regarding the definitions and implications of "rolling without slipping," particularly in relation to friction and momentum conservation. The discussion highlights the complexity of the physical scenario and the need for further clarification on the models being considered.
Similar threads
- · Replies 4 ·
- · Replies 7 ·
- · Replies 5 ·
- · Replies 1 ·
- · Replies 12 ·
- · Replies 9 ·
- · Replies 11 ·
- · Replies 5 ·
- · Replies 2 ·
- · Replies 13 ·