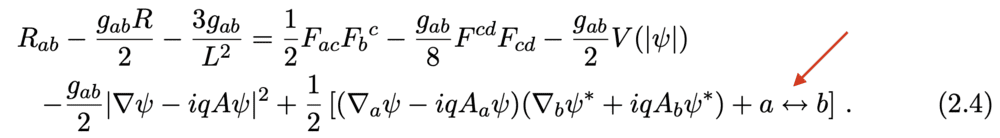SUMMARY
The left-right arrow notation ##a \leftrightarrow b## in the Einstein equation indicates the exchange of indices between terms, confirming the symmetry of the left-hand side (LHS) and right-hand side (RHS) of the equation. This notation is essential for understanding the implications of symmetry in tensor equations. The discussion highlights the importance of recognizing such notations in advanced physics papers, particularly in the context of general relativity and tensor calculus.
PREREQUISITES
- Understanding of Einstein's field equations
- Familiarity with tensor calculus
- Knowledge of symmetry principles in physics
- Basic comprehension of mathematical notation in physics
NEXT STEPS
- Research the implications of symmetry in Einstein's field equations
- Study tensor calculus applications in general relativity
- Explore advanced mathematical notations used in physics papers
- Learn about the significance of index notation in tensor analysis
USEFUL FOR
Physicists, students of general relativity, and anyone studying advanced mathematical physics will benefit from this discussion.