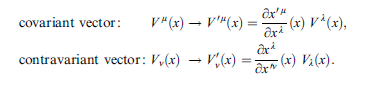SUMMARY
The discussion focuses on the transformation between Cartesian coordinates and polar coordinates, specifically addressing Lewis H. Ryder's method. A key point of confusion was identified regarding a sign typo in Ryder's definition of the variable ##r##, where the exponent should be ##1/2## instead of ##-1/2##. The participants clarified the calculation of partial derivatives, demonstrating that ##\frac{\partial x}{\partial r} = \cos\theta## and providing a pathway to complete the derivative of ##r## with respect to ##x##.
PREREQUISITES
- Understanding of Cartesian and polar coordinate systems
- Familiarity with partial derivatives in calculus
- Knowledge of trigonometric functions, specifically cosine
- Basic algebraic manipulation skills
NEXT STEPS
- Study the derivation of polar coordinates from Cartesian coordinates
- Learn about the properties and applications of partial derivatives
- Explore the implications of sign errors in mathematical definitions
- Practice problems involving transformations between coordinate systems
USEFUL FOR
Students and professionals in mathematics, physics, and engineering who are working with coordinate transformations and calculus.