thegirl
- 40
- 1
Hi I was wondering how you get this when taking the limit of T going to 0
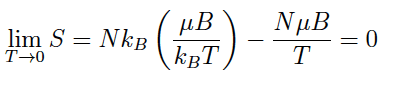
From this expression of S:
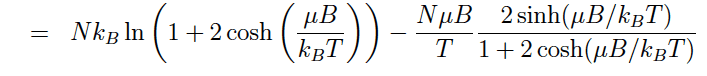
Please help I don't see how ln infinity goes to uB/KbT (used u to represent the greek letter. And how does the other expression of sinh and cosh approach 1?
From this expression of S:
Please help I don't see how ln infinity goes to uB/KbT (used u to represent the greek letter. And how does the other expression of sinh and cosh approach 1?