Linear Approximation: Check Your Answer

  • Context: MHB 
  • Thread starter Thread starter jaredjjj
  • Start date Start date
  • Tags Tags
    Approximation Linear
Click For Summary

Discussion Overview

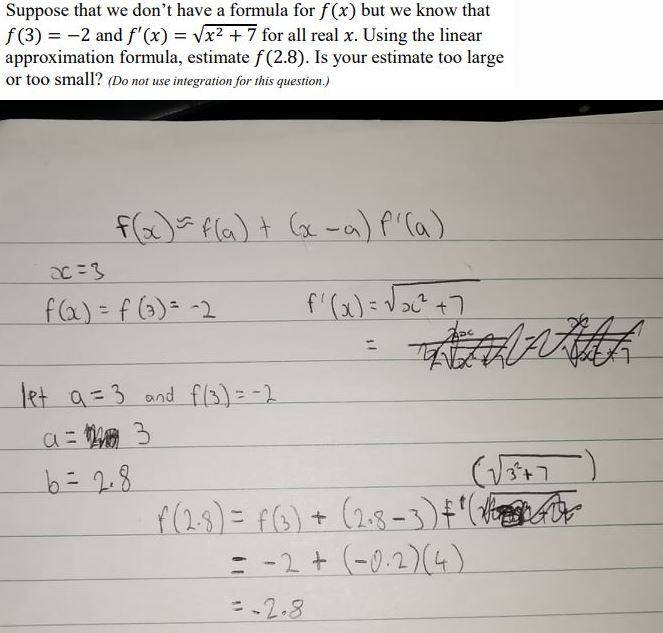
The discussion revolves around a linear approximation problem, specifically checking the correctness of a solution and determining whether the approximation is an overestimate or underestimate. Participants explore the implications of the derivative and the behavior of the function at a specific point.

Discussion Character

  • Technical explanation, Conceptual clarification, Debate/contested

Main Points Raised

  • One participant confirms that the linear approximation yields $f(2.8) \approx -2.8$.
  • Another participant questions how to determine if this approximation is an overestimate or underestimate.
  • There is a suggestion to use the derivative formula $f'(x)=\sqrt{x^2+7}$ to analyze the approximation further.
  • One participant states that using the derivative leads to the conclusion that $-2.8$ is approximately equal to $3.852$, which is claimed to be the same as $2.8$.
  • A participant notes that the linear approximation is a tangent line to $f(x)$ at the point $(3,-2)$ and asks about the significance of the second derivative $f''(3)$ in understanding the behavior of $f(x)$ at that point.

Areas of Agreement / Disagreement

Participants express agreement on the linear approximation result but have differing views on how to assess whether it is an overestimate or underestimate. The discussion remains unresolved regarding the implications of the second derivative.

Contextual Notes

There are missing assumptions regarding the function $f(x)$ and its derivatives, as well as unresolved steps in the reasoning about the relationship between the approximation and the actual function values.

jaredjjj
Messages
5
Reaction score
0
Have I solved this linear approximation question correctly?
Qqq6.JPG
 
Physics news on Phys.org
yes, $f(2.8) \approx -2.8$

now, how to determine if that value is an over or under estimate?
 
skeeter said:
yes, $f(2.8) \approx -2.8$

now, how to determine if that value is an over or under estimate?
To answer the second half do I have to use the formula f'(x)=sqrt(x^2+7) which would mean -2.8 would be approximately equal to 3.852 which is the same as 2.8.
 
jaredjjj said:
To answer the second half do I have to use the formula f'(x)=sqrt(x^2+7) which would mean -2.8 would be approximately equal to 3.852 which is the same as 2.8.

?

The linear approximation is a line tangent to $f(x)$ at the point $(3,-2)$.

What does the sign of $f''(3)$ tell you about the behavior of $f(x)$ at $x=3$ ?
 

Similar threads

High School Linearization of a function error viewed with differentials
  • · Replies 14 ·
Replies
14
Views
2K
High School Need some help with understanding linear approximations
  • · Replies 30 ·
2
Replies
30
Views
3K
Undergrad Approximation of a function of two variables
  • · Replies 3 ·
Replies
3
Views
2K
Undergrad Why can linear approximation equal quadratic approximation
  • · Replies 2 ·
Replies
2
Views
2K
High School Local Linear Approximation vs Linearization
  • · Replies 1 ·
Replies
1
Views
3K
MHB Monica's question at Yahoo Answers regarding Linear Approximation
  • · Replies 1 ·
Replies
1
Views
2K
MHB Estimate Paint for Hemispherical Dome - Linear Approximation
  • · Replies 1 ·
Replies
1
Views
2K
High School Mean-Value Theorem, Taylor's formula, and error estimation
  • · Replies 3 ·
Replies
3
Views
2K
Undergrad Problem with function approximation
  • · Replies 12 ·
Replies
12
Views
1K
MHB Dman's question at Yahoo Answers concerning linear approximates
  • · Replies 1 ·
Replies
1
Views
3K