mathmari
Gold Member
MHB
- 4,984
- 7
Hey! 
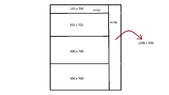
To product a product $3$ square plates $A$ with measures $300\times 500$mm and $2$ square plates $B$ with measures $400\times 600$mm are needed. These plates must be cut out by two different workpieces with measres $1000\times 1000$mm (Type I) and $600\times 1500$mm (Type II). The plates, for technology reason, must be cut through and no just cut in.
Totally $500$ products must be produced. The costs for the workpieces are proportional to their area, i.e., if a workpiece of Type I has the price 1, then a workpiece of Type II has the price $0.9$ ($1000000\ mm^2$ to $900000\ mm^2$).
There are $4$ possibilities, to cut plates A and/or B from a workpiece of Type I:
(1) 4A (scrap $16\%$)
(2) 3A, 1B (scrap $13\%$)
(3) 1A, 2B (scrap $31\%$)
(4) 3B (scrap $28\%$)
There are $3$ possibilities, to cut plates A and/or B from a workpiece of Type II:
(5) 4A ($8\%$ scrap)
(6) 2A, 2B (scrap $0\%$)
(7) 3B (scrap $24\%$)
Try to find these possibilities.
Formulate the problem as a linear optimization problem. Let $x_1, x_2, \ldots , x_7$ be the number of workpieces, that are necessary for the schemes (1), (2), ... , (7). The costs for the workpieces must be minimized.
What does it mean to find the possibilities? What do we have to do? Could you give me a hint? (Wondering)
To product a product $3$ square plates $A$ with measures $300\times 500$mm and $2$ square plates $B$ with measures $400\times 600$mm are needed. These plates must be cut out by two different workpieces with measres $1000\times 1000$mm (Type I) and $600\times 1500$mm (Type II). The plates, for technology reason, must be cut through and no just cut in.
Totally $500$ products must be produced. The costs for the workpieces are proportional to their area, i.e., if a workpiece of Type I has the price 1, then a workpiece of Type II has the price $0.9$ ($1000000\ mm^2$ to $900000\ mm^2$).
There are $4$ possibilities, to cut plates A and/or B from a workpiece of Type I:
(1) 4A (scrap $16\%$)
(2) 3A, 1B (scrap $13\%$)
(3) 1A, 2B (scrap $31\%$)
(4) 3B (scrap $28\%$)
There are $3$ possibilities, to cut plates A and/or B from a workpiece of Type II:
(5) 4A ($8\%$ scrap)
(6) 2A, 2B (scrap $0\%$)
(7) 3B (scrap $24\%$)
Try to find these possibilities.
Formulate the problem as a linear optimization problem. Let $x_1, x_2, \ldots , x_7$ be the number of workpieces, that are necessary for the schemes (1), (2), ... , (7). The costs for the workpieces must be minimized.
What does it mean to find the possibilities? What do we have to do? Could you give me a hint? (Wondering)