Liouville Master Equation for an Open Quantum System

[Raptor112]

By reading Heinz-Peter Breuer:

A Piece Wise Deterministic Process (where you have a deterministic time-evolution + a jump process and which is just a particular type of stochastic process) may be defined in terms of a Liouville master equation for its probability density :

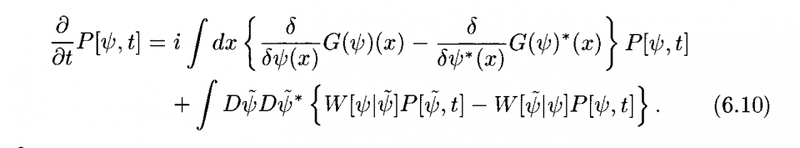
Where the first term is the deterministic term and the second term is the jump term.
So my questions are :
1. $P[\psi,t]$ is a probability functional so its a function of the wave function which is a function of what? time?
2. Is it also possible to relate this to the Lindblad Quantum Master Equation which is the most general master equation for an open Markovian system?

 

[DrClaude]

1. $P[\psi,t]$ is a probability functional so its a function of the wave function which is a function of what? time?

That depends on the quantum system. In the way it is represented there, at least position and time.

2. Is it also possible to relate this to the Lindblad Quantum Master Equation which is the most general master equation for an open Markovian system?

Yes. I don't have it with me now, but this is in the book by Breuer and Petruccione, Open Quantum Systems.

 

[A. Neumaier]

1. $P[\psi,t]$ is a probability functional so its a function of the wave function which is a function of what? time?
2. Is it also possible to relate this to the Lindblad Quantum Master Equation which is the most general master equation for an open Markovian system?

1. The wave function is a point in a projective Hilbert space. Sometimes the latter is a function space, sometimes not. Typically the small system part is parameterized in terms of position, whereas the detector part is parameterized in terms of occupation numbers for field modes. The big Hilbert space is the tensor product of both. The reduced Hilbert space in which the PDP lives is just that of the small system. If it is a nonrelativistic electron it is $L^2(R^3,C^2)$.

2. The Lindblad equation is obtained by averaging $\widehat\rho=\psi\psi^*$ over the realizations of the process for $\psi$. That's why the PDP is called an unraveling of the Lindblad equation.

 

[Raptor112]

I have been reading about unravelling the Lindblad quantum master equation for a while but I still do not have a firm grasp on the concept. My first question was why the word unravelling is used here as opposed to solving the equation? The Theory of Open Quantum Systems shows that the proof of the unravelling is achieved by differentiating the covariance matrix and showing the equation of motion for this matrix gives the Lindblad form, so is this equivalent to when you say:

2. The Lindblad equation is obtained by averaging ρ=ψψ∗\rho=\psi\psi^* over the measurement results. That's why the PDP is called an unraveling of the Lindblad equation.

 

[A. Neumaier]

I have been reading about unravelling the Lindblad quantum master equation for a while but I still do not have a firm grasp on the concept. My first question was why the word unravelling is used here as opposed to solving the equation? The Theory of Open Quantum Systems shows that the proof of the unravelling is achieved by differentiating the covariance matrix and showing the equation of motion for this matrix gives the Lindblad form, so is this equivalent to when you say:

When you cite something involving formulas with the quote button you need to edit the cited result to get the formulas correctly rendered! (If you cite the whole post with the reply button, this bug is absent.)

Taking the expectation over the classical realizations is the ''raveling''; undoing this is therefore called ''unraveling''. Unraveling is not a unique procedure since it depends on the details how the system is measured, while the (raveled) Lindblad equation is fairly independent of this.

Solving the equations is a completely different matter - it means obtaining an explicit (possibly approximate) form of the solution $\rho(t)$ or $\psi(t)$.

 

[Raptor112]

Taking the expectation over the classical realizations is the ''raveling''

What woul be the step by step process of averaging the solutions($\rho$) over all classical realizations(measurement results) as I seem to be having diffuclty grasping the concept of unravelling.

How would you actually average the density matrix over the measurements?

 

[A. Neumaier]

What would be the step by step process of averaging the solutions($\rho$) over all classical realizations(measurement results) as I seem to be having diffuclty grasping the concept of unravelling.

How would you actually average the density matrix over the measurements?

Not at all. One inserts the stochastic differential equation for $\psi$ into $(\psi\psi^*)^. =\dot\psi\psi^*+\psi\dot\psi^*$, then takes classical expectations to get a differential equation for $\rho=\langle\psi\psi^*\rangle$. This is the raveling process and gives a Lindblad equation. Conversely, to unravel a Lindblad equation one must guess the form of the stochastic process for $\psi$ and then show that raveling recovers the Lindblad equation. If you need further guidance, start doing this until you get stuck and then ask for further hints. Note that only one of the classical trajectories is actually realized through a continuous measurement of a single system; all others are fictitious in the sense in which Gibbs had introduced the concept of an ensemble.

 

[Raptor112]

Thanks a lot for that!

So does that mean when we actually solve(numerically or exactly) a Stochastic Schrödinger Equation to get the wavefunction, and then produce the density matrix we are actually solving the Lindblad equation?

Conversely, to unravel a Lindblad equation one must guess the form of the stochastic process for ψ\psi and then show that raveling recovers the Lindblad equation.

 

[A. Neumaier]

So does that mean when we actually solve(numerically or exactly) a Stochastic Schrödinger Equation to get the wavefunction, and then produce the density matrix we are actually solving the Lindblad equation?

If we solve the SSE numerically and then average $\psi\psi^*$ [not $\psi^*\psi$ as I had mistakenly written before, since this equals 1] over many realizations we get a good approximation to the density matrix. This is called the Monte Carlo wave function method, and is very useful when the dimension of the density matrix is large.

But solving an SSE exactly is usually significantly more diffcult than solving the corresponding Lindblad equation exactly.

 

[Raptor112]

So the answer to my question is yes?

 

[A. Neumaier]

So the answer to my question is yes?

yes, in the sense I indicated. But if you only make one simulation and form $\psi\psi^*$ you don't get a good approximation of $\rho$, though. The accuracy goes only like $O(N^{-1/2})$, as in all statistical methods.