Load applied at an angle -- how much force before breaking this die?

[Manganese]

Hello,
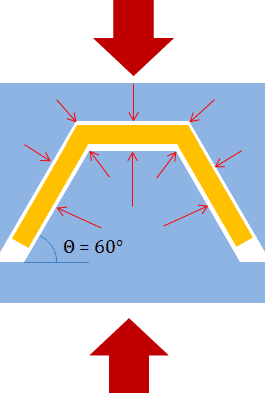
I was toying around with shapes and dies and wanted to calculate the load distribution in all spots so to get a rough idea of the maximum load I can use before breaking the die. The "problem" is as follows: I have a die shaped like a trapezium and I have to press an item (5-10mm thick) (yellow) in between. If the load is applied coaxially to the die, what is the pressure in the diagonal faces? (ignore the sharp edges, pretend they are rounded)

upper surface area, A1 = 70 x 70 mm = 4900 mm2
lower surface area, A2 = 70 x 70 mm = 4900 mm2
upper internal area, A3 = 30 x 70 mm = 2100 mm2
lower internal area, A4 = 23 x 70 mm = 1610 mm2
diagonal upper area, A5 = 40 x 70 mm = 2800 mm2
diagonal lower area, A6 = 33.96 x 70 = 2377.2 mm2
angle = 60°

The load is applied perpendicularly to the outer faces (A1 and A2) and is
F1 = 10000 N
so
P1 = P2 = 10000N/4900mm2 = 2.04 MPa (the pressure on the outer faces)

Since the internal faces, A3 and A4, are parallel to the outer faces A1 and A2, the force is also the same and so the pressures applied on the internal areas would be
P3 = 10000N/2100mm2 = 4.76 MPa
P4 = 10000N/1610mm2 = 6.21 MPa

Now, how is the load applied to the diagonal faces? And how much the pressure? Let's assume no attrition for ease, can this be treated the same as an object on an inclined plane?

In that case, the relative force perpendicular to the diagonal faces would be
F5 = F1⋅cosθ = 10000N*cos60° = 5000N
and the pressure on the diagonal faces would be
P5 = F5/A5 = 5000N/2800mm2 = 1.79 MPa
P6 = F5/A6 = 5000N/2377.2mm2 = 2.1 MPa

Is this conceptually correct? Of course in reality there is also attrition to take into account or nasty edges where stress is intensified, I just wanted to get a rough idea of how the load/stress is distributed (especially on the diagonal faces).

Or as the die is being pressed, the lower part will try to "open" the upper part and rip apart the two outer "triangles"? Does this fall under a specific topic on dies, presses etc? How do I look this up? Thanks

 

[jrmichler]

Does this fall under a specific topic on dies, presses etc? How do I look this up? Thanks

That depends on the process. If you are squashing a lump of material, the process is forging. If you are forming a sheet of material, the process is forming or sheet forming.

An excellent source for forming and forging is Manufacturing Processes for Engineering Materials, by Serope Kalpakjian. It is clearly written and easy to understand, with clear diagrams. My copy is a first edition with "only" 839 pages, while the latest 6th edition has over 1100 pages.