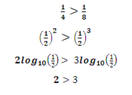Logarithm inequality divide an inequality by a negative value

Click For Summary

SUMMARY

The discussion centers on the mathematical principle that when dividing an inequality by a negative value, the direction of the inequality must be reversed. Specifically, the example provided illustrates that since $$\log_{10}\left(\frac{1}{2}\right)<0$$, dividing both sides of an inequality by this negative logarithmic value results in the reversed inequality, leading to the conclusion that $$2<3$$. This highlights a fundamental rule in inequality manipulation that is crucial for accurate mathematical reasoning.

PREREQUISITES

  • Understanding of logarithmic functions, specifically base 10 logarithms.
  • Familiarity with basic inequality properties in mathematics.
  • Knowledge of mathematical operations involving negative numbers.
  • Ability to manipulate and solve inequalities correctly.

NEXT STEPS

  • Study the properties of logarithms, focusing on their behavior with negative values.
  • Learn about inequality manipulation techniques in algebra.
  • Explore real-world applications of logarithmic inequalities in various fields.
  • Practice solving inequalities that involve logarithmic expressions and negative coefficients.

USEFUL FOR

Students, educators, and anyone interested in mastering algebraic concepts, particularly those dealing with logarithmic functions and inequalities.

highmath
Messages
35
Reaction score
0
What is error in the picture?
 

Attachments

  • logaritmquestion.PNG
    logaritmquestion.PNG
    7.9 KB · Views: 119
Mathematics news on Phys.org
The error arises because:

$$\log_{10}\left(\frac{1}{2}\right)<0$$

When we divide an inequality by a negative value, we need to reverse the direction of the inequality, so that we get:

$$2<3$$
 

Similar threads

Undergrad What Are the Benefits of Triangle Inequality in Mathematics?
  • · Replies 2 ·
Replies
2
Views
3K
High School What Are Basic Questions About Understanding Inequalities?
  • · Replies 12 ·
Replies
12
Views
2K
High School The same inequality, but two equivalent ways to express it
  • · Replies 14 ·
Replies
14
Views
2K
MHB Proof of Inequality: $|a+b| \leq |a| + |b|$
  • · Replies 8 ·
Replies
8
Views
3K
MHB Overcoming Struggles to Addressing Inequalities Step by Step
  • · Replies 3 ·
Replies
3
Views
1K
MHB Can You Solve This Challenging Inequality Problem?
  • · Replies 1 ·
Replies
1
Views
2K
Undergrad When does an inequality indicate a maximum or minimum value?
  • · Replies 8 ·
Replies
8
Views
2K
MHB Write an inequality and solve for the maximum possible value of n
  • · Replies 5 ·
Replies
5
Views
2K
Undergrad Understanding Cauchy-Schwarz Inequality
  • · Replies 7 ·
Replies
7
Views
2K
MHB Solve Inequality & Simul Eqns: Alg Workings Q (a,b,c)
  • · Replies 1 ·
Replies
1
Views
2K