dynamicskillingme
- 26
- 0
Homework Statement
Has solution
It then goes on to state the solution blows up at
My issue is when I do the solution I get
(Working)
The discussion centers on understanding the Lipshitz condition in the context of solving the differential equation \(\dot{y} = y^2\). Participants clarify that \(y\) is a function of \(t\) and emphasize the importance of correctly applying integration techniques. The solution \(y(t) = \frac{y_0}{1 - y_0 t}\) is validated by substituting it back into the original differential equation. Key techniques for proving solutions include understanding derivatives and the method of separation of variables.
PREREQUISITESStudents in engineering or mathematics who are tackling differential equations, particularly those seeking to solidify their understanding of integration and solution verification techniques.
dynamicskillingme said:\dot{y} = y^2
y = yt + c ; for t = 0
dynamicskillingme said:Homework Statement
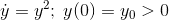
Has solution
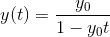
It then goes on to state the solution blows up at, which I understand.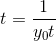
My issue is when I do the solution I get
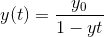
(Working)
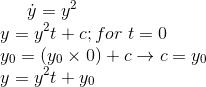
dynamicskillingme said:How could I prove their answer, or what should I read up on to be able to show this proof?