Magnetic field due to infinite plane

[Saitama]

Homework Statement

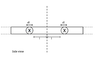
Find the magnitude and direction of the magnetic induction vector $\textbf{B}$ of an infinite plane carrying a current of linear density $\textbf{i}$; the vector $\textbf{i}$ is same at all points of the plane.

Homework Equations

The Attempt at a Solution

I can do this with integration but I have seen the same question solved before. The solution was done using Ampere's circuital law. I seem to have forgotten the way it was solved. How can I do this using Ampere's circuital law. I don't even have the slightest idea about what shape should be the amperian loop.

If we divide the plane into thin infinite current carrying wire and consider wires at equal distances from the symmetrical axis, it can be deduced from symmetry that the direction of magnetic field is downwards towards the plane.

Thanks!

 

[rude man]

The following may be something like what you had in mind, so forgive any redundant observations, but:

Could you not run a rectangular Amperian loop around a section of plane of length L and depth D, D << L. The depth dimension penetrates the sheet on both sides. So then the current thru this loop is i*L and ampere's law gives 2L*H = i*L. The H field is parallel to the sheet but perpendicular to i everywher which is what I think you also concluded, with H = i/2, i in amp/m. The H field points in opposite directions on opposite sides of the plane.

 

[Saitama]

Sorry for the late reply.

The following may be something like what you had in mind, so forgive any redundant observations, but:

Could you not run a rectangular Amperian loop around a section of plane of length L and depth D, D << L. The depth dimension penetrates the sheet on both sides. So then the current thru this loop is i*L and ampere's law gives 2L*H = i*L. The H field is parallel to the sheet but perpendicular to i everywher which is what I think you also concluded, with H = i/2, i in amp/m. The H field points in opposite directions on opposite sides of the plane.

Thanks rude man, that worked!

I did not conclude that the direction of field is perpendicular to $i$ but instead I said that it is perpendicular to the plane of infinite sheet which is completely wrong.

Thank you!