Magnetic field due to semi-circular wire

[ks_wann]

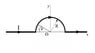
So, I've got a wire with a semicircle about the origin, my task is to find the magnetic field at M=(0,0,z).

I want to use Biot-Savart, so I find dl', r and r-hat. (r being the vector from the source point to field point)



\begin{equation}
r^{2}=R^{2}+z^{2}\\
\mathbf{r}=R\cos{\theta}\mathbf{\hat{i}}+R\sin{\theta}\mathbf{\hat{j}}+z\mathbf{\hat{k}}\\
d\mathbf{l^{\prime}}=Rd\theta \mathbf{\hat{\theta}}

\end{equation}

With these identified, I use biot-savart:

\begin{equation}
\mathbf{B}(\mathbf{r})=\frac{\mu_{0}I}{4\pi}\int\frac{d\mathbf{l^{ \prime}}\times\mathbf{\hat{r}}}{r^{2}}
\end{equation}


What troubles me is the cross product. I get

\begin{equation}
d\mathbf{l^{\prime}}\times\mathbf{\hat{r}}=\frac{R}{\sqrt{R^{2}+z^{2}}} \mathbf{\hat{\theta}}\times(R\cos\theta \mathbf{\hat{i}}+R\sin\theta \mathbf{\hat{j}}+z\mathbf{\hat{k}})
\end{equation},

and I'm not sure what to make of it as the unit vector would change all the way through the semicircle.

 

[nrqed]

This is a case where the angle between \vec{dl'} and \hat{r} is always the same so it is much better to simply use the right hand rule to find the direction and use dl' \, \sin \theta to find the magnitude. If you absolutely want to use a cross product, write instead \vec{dl'} as dl' \, \hat{\theta}.

 

[ks_wann]

Okay. So I basically just state that the field points downwards in the case of z=0, and get
\begin{equation} \frac{\mu_0I}{4\pi} \int_{\theta_{1}}^{\theta^{2}} \frac{R}{(R^2+z^2)^{3/2}} \sin{\theta} d \theta \end{equation}?

What about the change in direction with increasing z?

 

[unscientific]

Consider a small segment of the wire of length $d\vec l$, producing a small magnetic flux density $d\vec B$ at position $\vec r$ away from the wire.

Hint: what can you say about the direction of $d\vec l$ and $\hat r$?

Also, expressing $dl = R \space d\phi$ will make your integral much easier. Exploit symmetries instead of diving straight into Cartesian cross products..

 

[ks_wann]

Consider a small segment of the wire of length $d\vec l$, producing a small magnetic flux density $d\vec B$ at position $\vec r$ away from the wire.

Hint: what can you say about the direction of $d\vec l$ and $\hat r$?

Well, $d\vec l$ and $\hat r$ are perpendicular at all times. I see that for a full circle, all the horizontal components will cancel, thus giving me $B(z)$. Am I missing something?

I'm sadly not very good at identifying and exploiting symmetries..

 

[unscientific]

Well, $d\vec l$ and $\hat r$ are perpendicular at all times. I see that for a full circle, all the horizontal components will cancel, thus giving me $B(z)$. Am I missing something?

I'm sadly not very good at identifying and exploiting symmetries..

Yes horizontal components cancel for a full circle, but not for a semi-cricle. Do the integration for horizontal and components separately.