Nick89
- 553
- 0
Hi,
I was hoping someone can verify this for me.
In uni today we had to calculate the magnetic field of a ring of current, lying in the xy-plane. First we had to calculate it on the z-axis (perpendicular to the ring) which was easy.
Then we had to calculate it on the y-axis (in the plane of the ring, outside of the ring). Because this was apparently too hard however, we had to 'simplify' the ring into a square, which made the calculation almost childlishly easy...
I was wondering now why they thought it was so hard... I tried to calculate it with an actual ring and the only difficulty I had was to calculate the integral, which was pretty ugly when calculated with Maple...
If someone can verify my calculation for me please that would be great.
Consider the following diagram, a loop (blue) with radius R lying in the xy-plane with a current I traveling in the direction of the vector dl.
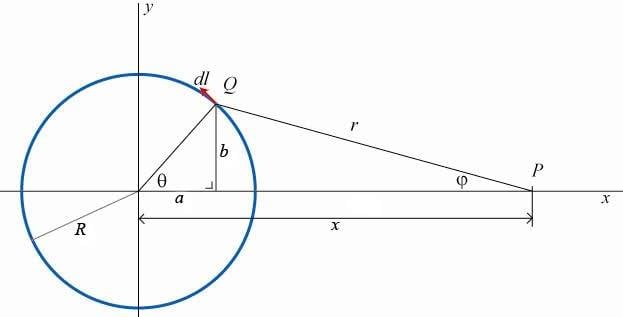
I want to calculate the magnetic field on the point P lying on the x-axis, a distance x from the origin, using Biot-Savart's law:
d \vec{B} = \frac{ \mu_0 }{4 \pi} \frac{I d\vec{l} \times \hat{r}}{r^2} where \hat{r} is the direction of \vec{r}.
Since r is dependend on \theta, I have to find a way to link them.
What I did was:
a = R \sin\theta \text{ , } b = R \cos\theta
r^2 = b^2 + (x-a)^2 = (R \cos\theta)^2 + (x - R\sin\theta)^2
Finally, (the part where I'm not entirly sure), I figured dl = R d\theta for a small angle d\theta.
This finally yields (the direction is obvious):
B = \frac{ \mu_0 I}{4 \pi} \int_0^{2 \pi} \frac{ R d\theta }{(R \cos\theta)^2 + (x - R\sin\theta)^2}
For the integral, I didn't even try to do it manually but had Maple do it. The answer was:
\int_0^{2 \pi} \frac{ R d\theta }{(R \cos\theta)^2 + (x - R\sin\theta)^2}=-2\,iR \left( \ln \left( {\frac {i \left( {x}^{2}+{R}^{2} \right) }{-<br /> {x}^{2}+{R}^{2}}} \right) -\ln \left( {\frac {-i \left( {x}^{2}+{R}^{<br /> 2} \right) }{-{x}^{2}+{R}^{2}}} \right) \right) \left( -{x}^{2}+{R}^<br /> {2} \right) ^{-1}
(Yikes...)
Am I right on this? If so, I can't understand why we had to imagine the ring as a square (apart from the horrible integral)... It made the calculation completely different (upper and lower portion of the square cancel, remaining two lines are simply two lines, add up the fields...)
And we get horrible integrals all the time, the question just states that we don't have to calculate it then...
So yeah, thanks if anyone can verify or tell me where I went wrong!
I was hoping someone can verify this for me.
In uni today we had to calculate the magnetic field of a ring of current, lying in the xy-plane. First we had to calculate it on the z-axis (perpendicular to the ring) which was easy.
Then we had to calculate it on the y-axis (in the plane of the ring, outside of the ring). Because this was apparently too hard however, we had to 'simplify' the ring into a square, which made the calculation almost childlishly easy...
I was wondering now why they thought it was so hard... I tried to calculate it with an actual ring and the only difficulty I had was to calculate the integral, which was pretty ugly when calculated with Maple...
If someone can verify my calculation for me please that would be great.
Consider the following diagram, a loop (blue) with radius R lying in the xy-plane with a current I traveling in the direction of the vector dl.
I want to calculate the magnetic field on the point P lying on the x-axis, a distance x from the origin, using Biot-Savart's law:
d \vec{B} = \frac{ \mu_0 }{4 \pi} \frac{I d\vec{l} \times \hat{r}}{r^2} where \hat{r} is the direction of \vec{r}.
Since r is dependend on \theta, I have to find a way to link them.
What I did was:
a = R \sin\theta \text{ , } b = R \cos\theta
r^2 = b^2 + (x-a)^2 = (R \cos\theta)^2 + (x - R\sin\theta)^2
Finally, (the part where I'm not entirly sure), I figured dl = R d\theta for a small angle d\theta.
This finally yields (the direction is obvious):
B = \frac{ \mu_0 I}{4 \pi} \int_0^{2 \pi} \frac{ R d\theta }{(R \cos\theta)^2 + (x - R\sin\theta)^2}
For the integral, I didn't even try to do it manually but had Maple do it. The answer was:
\int_0^{2 \pi} \frac{ R d\theta }{(R \cos\theta)^2 + (x - R\sin\theta)^2}=-2\,iR \left( \ln \left( {\frac {i \left( {x}^{2}+{R}^{2} \right) }{-<br /> {x}^{2}+{R}^{2}}} \right) -\ln \left( {\frac {-i \left( {x}^{2}+{R}^{<br /> 2} \right) }{-{x}^{2}+{R}^{2}}} \right) \right) \left( -{x}^{2}+{R}^<br /> {2} \right) ^{-1}
(Yikes...)
Am I right on this? If so, I can't understand why we had to imagine the ring as a square (apart from the horrible integral)... It made the calculation completely different (upper and lower portion of the square cancel, remaining two lines are simply two lines, add up the fields...)
And we get horrible integrals all the time, the question just states that we don't have to calculate it then...
So yeah, thanks if anyone can verify or tell me where I went wrong!