How Does Electron Behavior Influence the Magnetic Field in Copper Wires?

[taylaron]

when you run electricity through a wire it creates a magnetic field which is proportional to the amount of electricity flowing through it.
At the subatomic level, you've got a whole bunch of copper atoms, each surrounded by orbiting electrons. flowing electricity is the "switching" of these electrons from one neighbor atom the other.
in any wire (that isn't one atom in diameter) electrons flow in a general straight line. thus you have current. but within the wire; electrons are being "switched". but i don't think that it would be safe to assume that the switching is taking place with atoms in a straight line. my point is you've got electrons not always "switching" in a straight line. you result in a minuscule electromagnetic field that is not oriented in the same way the magnetic field of the electrons switching in a straight line.
if you've got a whole bunch of these transfer's going on in a wire; wouldn't that decrease the size of the magnetic field in the big picture (that the copper wire is generating as a "whole")?


I've come up with a concept that I am curious whether it is true or not.
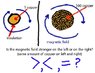
My idea is that you've got a 100 gauge copper wire with insulation around it; when you run x amount of electricity through it, it produces a magnetic field around the wire.
then you take 100, 1 gauge wire covered in an ultra-thin insulator, then you run x/100 electricity through each wire.

you end up with 1 big insulated wire and one insulated wire with 100 smaller "configurations" within it.

thanks. forgive the crude drawing

 

[TMM]

A few initial corrections:

I assume by electricity you mean voltage, I'll substitute V for x. Also gauge is a weird measurement with some subtleties, by what you're saying, I assume you mean that the large wire has 100 times the area of the little wires.

Anyway:

The magnetic field should be stronger in the single wire because resistance is resistivity*length/area. In other words, the resistance of each of the little wires is greater.

Let's call resistivity r and length L and say that the area of each little wire is 0.01, so:

Current of each little wire = (V/100)/(rL*100) = (V/rL)/10000

Magnetic field strength is directly proportional to that, multiply it by 100 to get the total field strength of the little wires:

B(little wires) = k(V/rL)/100

For the big wire:

Resistance = rL/(100*0.01) = rL

Current = V/rL

B(Big wire) = k(V/rl)

So we have B(Big Wire) : B(Little wires) = 100: 1

 

[marcusl]

A few corrections are in order. First, electrons don't jump from atom to atom in a metal, rather the electrons in the conduction shell are free to travel through the copper crystal lattice in much the same way as high speed basketballs could travel through a forest that has clear lanes running between the trees. Resistance in the wire comes from crystal imperfections (if some trees are growing in the lanes instead, the balls will ricochet off them in random directions) and from thermal agitation (as though the trees are moving randomly around their average positions, again causing collisions). At equilibrium the instantaneous electron speeds in a wire are gigantic but directed randomly so no current flows. If a voltage is applied to the wire, however, the otherwise random motions on average favor the direction of electric field and a net drift in one direction occurs. This small drift is the electric current.

Second, wire gauge works opposite your example. Small numbers are big wires. 36AWG is a tiny wire like a hair, 4 is the size used for automobile battery connections.

Third, magnetic field depends only on the current flowing. So long as you arrange for the same current to flow in the single fat wire or in the sum of the many small ones, the magnetic field outside will be equal. In fact, the field is the same if you flow the same current in a single fat wire and in a single skinny one.