How Is the Force on a Mass Moving Along a Frictionless Half-Circle Calculated?

[spizma]

Homework Statement

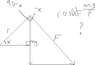
A small particle of mass m is pulled to the top of a frictionless
half-cylinder (of radius r) by a cord that passes
over the top of the cylinder, as illustrated in Figure
P7.20. (a) If the particle moves at a constant speed, show
that F = mg*cos(x). (Note: If the particle moves at constant
speed, the component of its acceleration tangent to the
cylinder must be zero at all times.)

See picture 1

Homework Equations

Force of gravity = mg

cos(x)=adj/hyp

The Attempt at a Solution

Well I figured that what you really need to do is find an equation giving the force vector of the particle. Picture 2 illustrates what I figured. The smaller triangle is the one from the half circle. The larger triangle is for the force vector of the triangle. Because the force vector is tangent to the circle, the radius must be perpendicular with the force vector. From there you can find the top angle of the large triangle. From that you can write cos(x)= mg/F. That gives you F = mg/cos(x), which is wrong. This has been bothering me for a while. The solution is probably something very simple I'm just missing. Could someone please help?

 

[spizma]

Well, to anyone who is willing to help, I have to go to bed and I won't be able to be here again until early afternoon tomorrow, so don't expect a response back until then.

 

[Dick]

That's the usual problem with posting figures to be approved. I suspect you have confused the triangle of the positional geometry with the triangle of the force geometry, but I was waiting you see your pictures. G'night.

 

[andrevdh]

Some hints:

There is another force acting on the particle, the normal force, but it is not relevant to the getting the answer.

Since it is being pulled upwards F should point in the opposite direction.

Consider the fact that the tangential forces (components) needs to be in equilibrium.

 

[Kushal]

you are pulling the mass from the other side of the half cylinder right?

what is the resultant force acting on the mass at any point?

be careful when resolving the vectors.

also, it says the mass moves with constant velocity. resultant acceleration is zero.
what does this imply about resultant force?

 

[Dick]

You've drawn the force diagram wrong. F and mg don't have the same vertical component. There are three forces acting on the mass. F, a normal force N and gravity. F+N=mg. F and N are perpendicular. mg is vertical. mg is the HYPOTENUSE.

 

[spizma]

Thank you!

Alright I figured out what I was doing wrong, and how to get the right answer (F=mg*cos(x)). Thanks Dick and everyone else for the help!