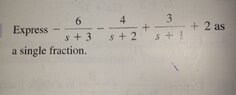SUMMARY
The discussion focuses on solving algebraic fractions, specifically the expression $$-\frac{6}{s+3}-\frac{4}{s+2}+\frac{3}{s+1}+2$$. The key steps involve determining the lowest common denominator (LCD) and rewriting each term to have this common denominator. The final combined expression is $$\frac{-6(s+2)(s+1)-4(s+3)(s+1)+3(s+3)(s+2)+2(s+3)(s+2)(s+1)}{(s+3)(s+2)(s+1)}$$, which can be further simplified by expanding and combining like terms.
PREREQUISITES
- Understanding of algebraic fractions
- Knowledge of lowest common denominator (LCD) concepts
- Ability to manipulate rational expressions
- Familiarity with polynomial expansion and simplification
NEXT STEPS
- Practice solving complex algebraic fractions with multiple terms
- Learn techniques for finding the lowest common denominator in rational expressions
- Explore polynomial expansion methods for simplifying expressions
- Study the properties of rational functions and their applications
USEFUL FOR
Students learning algebra, educators teaching algebraic concepts, and anyone looking to improve their skills in manipulating rational expressions.