Math Manipulation: Why Does l Approach Infinity?

[sparkle123]

Why does

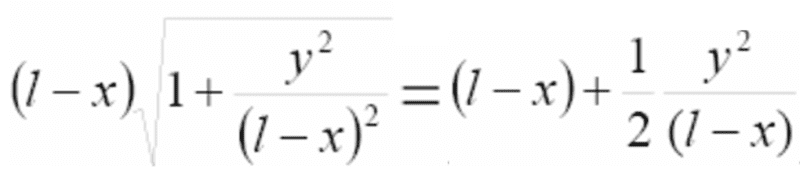
when l approaches infinity?
This would mean that

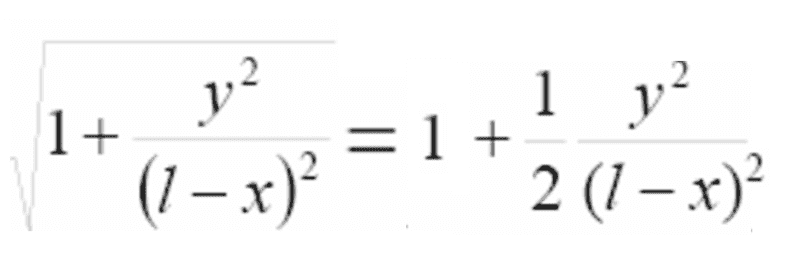but I don't understand why that would be true.
Thanks!

 

[Dick]

sqrt(1+r)=1+r/2-r^2/8+... That's the Taylor series expansion of sqrt(1+r). If r is small, then 1+r/2 is a good approximation. And as l->infinity then y^2/(l-x)^2 becomes very small. The sides aren't equal for any finite l. But the approximation becomes better and better as l->infinity.

 

[ehild]

Try it: Calculate the square root of 1+x with smaller and smaller x-values. For example, √1.2=1.095, √1.02=1.0099, √1.002=1.000999...

\sqrt{1+x} \approx 1+x/2

ehild

 

[sparkle123]

Thank you Dick and ehild! :)