Mathematica - using NIntegrate within NDSolve

[maves]

Hello,
I am computing orbits of constant energy in a gravitational potential of a complicated planet (sth like a torus).

I need to solve a system of 2nd order differential equations, that look something like
$$\ddot x=-\frac{\partial \phi}{\partial x}$$ and the same for y and z. The problem is that ∅ is a complicated integral that can not be solved analitically. I transformed the system of equations to a system of 1st order equations using new variables x1, x2, y1, y2, z1, z2 (is that even necessary?) and tried to solve them using NDSolve. The solutions I am looking for should be lying in particular planes, so I put for instance z=0 and then defined the integrals (already partially derived):

int1[x1_?NumericQ, y1_?NumericQ] :=
NIntegrate[((R (x1 - R Cos[\[Phi]]))/((x1 - R Cos[\[Phi]])^2 + (y1 - R Sin[\[Phi]])^2 + (0 -
Z)^2))^(3/2), {\[Phi], 0, 2 Pi}, {R, b, b + c}, {Z, R-(b+c), -R + (b + c)}];
int2[x1_?NumericQ, y1_?NumericQ] :=
NIntegrate[((R (y1 - R Sin[\[Phi]]))/((x1 - R Cos[\[Phi]])^2 + (y1 - R Sin[\[Phi]])^2 + (0 -
Z)^2))^(3/2), {\[Phi], 0, 2 Pi}, {R, b, b + c}, {Z, R-(b+c), -R + (b + c)}];

and then used these in NDSolve:
s = NDSolve[{
x1'[t] == x2[t],
y1'[t] == y2[t],
x2'[t] == int1[x1[t], y1[t]],
y2'[t] == int2[x1[t], y1[t]],
x1[0] == 9.6, x2[0] == 0, y1[0] == 0, y2[0] == 1.52}, {x1, x2, y1,
y2}, {t, 0, 100}][[1]],

having chosen some random initial values (well, not exactly random, I believe x1-the initial position in direction x - should be close to the planet (9.5), y1 is not needed and y2 - the initial velocity in direction y - should be "something") .

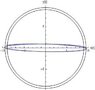
I plotted the solutions {x(t),y(t)}:
ParametricPlot[Evaluate[{x[t], y[t]} /. s], {t, 0, 100},
PlotRange -> All, AxesOrigin -> {0, 0},
AxesLabel -> {"x1[t]", "y1[t]"}]

which is the trajectory of a particle in my gravitational potential ∅. The initial instruction tells me to find the orbits of lowest (constant) energy (so, as I understand, by changing the initial conditions/values), but when I plot my solutions, I always get a linear line, now matter what i put into the initial values. I don't know, whether the problem is in my understanding of the problem, the part written in Mathematica or somewhere else. I would be very glad if anyone could help me out, and I apologize for the long post, I hope I made it clear, what the problem is.

 

[maves]

So I still have hope, that maybe someone could help me :) What I figured out until now is, that i forgot to take into account one minus sign, which made everything wrong, as the gravitational force in my calculations was repulsive and so the trajectory was hyperbolic (looked like linear on first sight). I also left the expression in the second-order form.

So, the right expressions for integrals in xy plane are:
1) Firstly, I define the first integral, which is equal to $-\frac{\partial \phi}{\partial x}$: (This "?NumericQ" must be here, if I want the program to proceed without evaluating the integral for a specific value of x and y. I integrate over $\Phi, R, Z$ and leave x and y "free", so that I will be able to evaluate the integrals at the points that NDSolve will calculate.

int1[x_?NumericQ, y_?NumericQ] :=
NIntegrate[((R (x - R Cos[\[Phi]]))/((x - R Cos[\[Phi]])^2 + (y - R Sin[\[Phi]])^2 + (0 -
Z)^2))^(3/2), {\[Phi], 0, 2 Pi}, {R, b, b + c}, {Z, R-(b+c), -R + (b + c)}];

2) Similarly, I define the second integral, which is equal to $-\frac{\partial \phi}{\partial y}$:

int2[x_?NumericQ, y_?NumericQ] :=
NIntegrate[((R (y - R Sin[\[Phi]]))/((x - R Cos[\[Phi]])^2 + (y - R Sin[\[Phi]])^2 + (0 -
Z)^2))^(3/2), {\[Phi], 0, 2 Pi}, {R, b, b + c}, {Z, R-(b+c), -R + (b + c)}];

Now I can write my set of equations and set the initial values, for instance:

s = NDSolve[{
x''[t] == int1[x[t], y[t]],
y''[t] == int2[x[t], y[t]],
x[0] == 9.6, x'[0] == 0, y[0] == 0, y'[0] == 1.5}, {x, x', y,
y'}, {t, 0, 10}][[1]]



And plot my solutions:
ParametricPlot[Evaluate[{x[t], y[t]} /. s], {t, 0, 10}]

x[0] has been chosen close to the toroid (9.5), because the potential is lowest near the toroid. The orbits in xy plane should be circular and go "around" the torus (like a satellite).
For comparison, I also plotted the torus in the xy plane, as the orbits should be circular or at least elliptical, and they seem completely wrong - like if there was no torus at all, they cross the planet, which is of course wrong - something like the case shown in attachment, remember, this is the xy plane!

I would be very glad if anyone could help me here - is there anything wrong with my code? but what could it be, as the code is not exactly rocket science -; or at least tell me, if you think my thread was posted to the wrong section.