- #1
maves
- 17
- 0
Hello,
I am computing orbits of constant energy in a gravitational potential of a complicated planet (sth like a torus).
I need to solve a system of 2nd order differential equations, that look something like
[tex]\ddot x=-\frac{\partial \phi}{\partial x}[/tex] and the same for y and z. The problem is that ∅ is a complicated integral that can not be solved analitically. I transformed the system of equations to a system of 1st order equations using new variables x1, x2, y1, y2, z1, z2 (is that even necessary?) and tried to solve them using NDSolve. The solutions I am looking for should be lying in particular planes, so I put for instance z=0 and then defined the integrals (already partially derived):
int1[x1_?NumericQ, y1_?NumericQ] :=
NIntegrate[((R (x1 - R Cos[\[Phi]]))/((x1 - R Cos[\[Phi]])^2 + (y1 - R Sin[\[Phi]])^2 + (0 -
Z)^2))^(3/2), {\[Phi], 0, 2 Pi}, {R, b, b + c}, {Z, R-(b+c), -R + (b + c)}];
int2[x1_?NumericQ, y1_?NumericQ] :=
NIntegrate[((R (y1 - R Sin[\[Phi]]))/((x1 - R Cos[\[Phi]])^2 + (y1 - R Sin[\[Phi]])^2 + (0 -
Z)^2))^(3/2), {\[Phi], 0, 2 Pi}, {R, b, b + c}, {Z, R-(b+c), -R + (b + c)}];
and then used these in NDSolve:
s = NDSolve[{
x1'[t] == x2[t],
y1'[t] == y2[t],
x2'[t] == int1[x1[t], y1[t]],
y2'[t] == int2[x1[t], y1[t]],
x1[0] == 9.6, x2[0] == 0, y1[0] == 0, y2[0] == 1.52}, {x1, x2, y1,
y2}, {t, 0, 100}][[1]],
having chosen some random initial values (well, not exactly random, I believe x1-the initial position in direction x - should be close to the planet (9.5), y1 is not needed and y2 - the initial velocity in direction y - should be "something") .
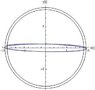
I plotted the solutions {x(t),y(t)}:
ParametricPlot[Evaluate[{x[t], y[t]} /. s], {t, 0, 100},
PlotRange -> All, AxesOrigin -> {0, 0},
AxesLabel -> {"x1[t]", "y1[t]"}]
which is the trajectory of a particle in my gravitational potential ∅. The initial instruction tells me to find the orbits of lowest (constant) energy (so, as I understand, by changing the initial conditions/values), but when I plot my solutions, I always get a linear line, now matter what i put into the initial values. I don't know, whether the problem is in my understanding of the problem, the part written in Mathematica or somewhere else. I would be very glad if anyone could help me out, and I apologize for the long post, I hope I made it clear, what the problem is.
I am computing orbits of constant energy in a gravitational potential of a complicated planet (sth like a torus).
I need to solve a system of 2nd order differential equations, that look something like
[tex]\ddot x=-\frac{\partial \phi}{\partial x}[/tex] and the same for y and z. The problem is that ∅ is a complicated integral that can not be solved analitically. I transformed the system of equations to a system of 1st order equations using new variables x1, x2, y1, y2, z1, z2 (is that even necessary?) and tried to solve them using NDSolve. The solutions I am looking for should be lying in particular planes, so I put for instance z=0 and then defined the integrals (already partially derived):
int1[x1_?NumericQ, y1_?NumericQ] :=
NIntegrate[((R (x1 - R Cos[\[Phi]]))/((x1 - R Cos[\[Phi]])^2 + (y1 - R Sin[\[Phi]])^2 + (0 -
Z)^2))^(3/2), {\[Phi], 0, 2 Pi}, {R, b, b + c}, {Z, R-(b+c), -R + (b + c)}];
int2[x1_?NumericQ, y1_?NumericQ] :=
NIntegrate[((R (y1 - R Sin[\[Phi]]))/((x1 - R Cos[\[Phi]])^2 + (y1 - R Sin[\[Phi]])^2 + (0 -
Z)^2))^(3/2), {\[Phi], 0, 2 Pi}, {R, b, b + c}, {Z, R-(b+c), -R + (b + c)}];
and then used these in NDSolve:
s = NDSolve[{
x1'[t] == x2[t],
y1'[t] == y2[t],
x2'[t] == int1[x1[t], y1[t]],
y2'[t] == int2[x1[t], y1[t]],
x1[0] == 9.6, x2[0] == 0, y1[0] == 0, y2[0] == 1.52}, {x1, x2, y1,
y2}, {t, 0, 100}][[1]],
having chosen some random initial values (well, not exactly random, I believe x1-the initial position in direction x - should be close to the planet (9.5), y1 is not needed and y2 - the initial velocity in direction y - should be "something") .
I plotted the solutions {x(t),y(t)}:
ParametricPlot[Evaluate[{x[t], y[t]} /. s], {t, 0, 100},
PlotRange -> All, AxesOrigin -> {0, 0},
AxesLabel -> {"x1[t]", "y1[t]"}]
which is the trajectory of a particle in my gravitational potential ∅. The initial instruction tells me to find the orbits of lowest (constant) energy (so, as I understand, by changing the initial conditions/values), but when I plot my solutions, I always get a linear line, now matter what i put into the initial values. I don't know, whether the problem is in my understanding of the problem, the part written in Mathematica or somewhere else. I would be very glad if anyone could help me out, and I apologize for the long post, I hope I made it clear, what the problem is.