Max Fidelity at $$F=|\langle\psi|\phi\rangle|^2$$

[deepalakshmi]

TL;DR

I have two pure states i.e. initial state and final state. I should get Fidelity as 1 when #t=\pi{/2}#
But I am not getting. What is wrong in my calculation?

$$F =|\langle\psi|\phi \rangle|^2$$
$$|\psi\rangle=|\alpha\rangle|0\rangle$$
$$|\phi\rangle= |\cos(t)\alpha\rangle|i\alpha\sin(t)\rangle$$
$$F=|(|\langle\alpha|\langle 0|)(|\cos(t)\alpha\rangle|i\alpha\sin(t)\rangle)|^2$$
Now simplifying $$\langle\alpha|\cos(t)\alpha\rangle$$
$$=e^{-\frac{|\alpha|^2}{2}}\sum_{n=0}\frac{(\alpha^\ast)^n}{\sqrt{n!}}\langle n|e^{-\frac{|\alpha\cos(t)|^2}{2}}\sum_{m=0}\frac{(\alpha\cos(t))^m}{\sqrt{m!}}|m\rangle$$
$$=e^{-\frac{|\alpha|^2}{2}}e^{-\frac{|\alpha\cos(t)|^2}{2}}\sum_{n=0}\sum_{m=0}\frac{(\alpha^\ast\alpha\cos(t))^n}{\sqrt{n!}}\langle n|m\rangle$$
$$=e^{{-|\alpha|^2}{/2}}e^{{-|\alpha\cos(t)|^2}{/2}}e^{|\alpha|^2\cos(t)}$$
Now simplifying $$\langle 0|i\sin(t)\alpha\rangle$$
$$=\langle 0| e^{-\frac{|\alpha\sin(t)|^2}{2}}\sum_{n=0}\frac{(\alpha i\sin(t))^n}{\sqrt{n!}}|n\rangle $$
$$=e^{-\frac{|\alpha\sin(t)|^2}{2}}$$
$$F=|e^{{-|\alpha|^2}{/2}}e^{{-|\alpha\cos(t)|^2}{/2}}e^{|\alpha|^2\cos(t)}e^{-\frac{|\alpha\sin(t)|^2}{2}}|^2$$
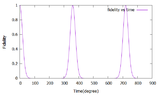
Now when t=0 , I am getting F=1.
when $t=\pi{/2}$ I am getting F= (4.5)(10^-5)
But my teacher says that even at #t=\pi{/2}#, I should get F=1. Here alpha is the coherent state and its value is sqrt5
Why should I get 1 and Why am i not getting 1?

What's wrong with my calculation?

 

[Demystifier]

Have you resolved your errors in your previous calculation of the same type?

 

[deepalakshmi]

Have you resolved your errors in your previous calculation of the same type?

yes. I have done

 

[Demystifier]

I see no error, but your final expression can be simplified as
$$F=e^{-2|\alpha|^2(1-\cos t)}$$
This is 1 for $t=2\pi$, maybe that's what your teacher meant?

 

[deepalakshmi]

No. He clearly told me I should get 1 at t= #/pi /2#.

 

[Demystifier]

Sometimes even teachers make errors.

 

[deepalakshmi]

Is there any theory that I should get constant fidelity for pure state even in different degrees i.e.0,90etc

 

[deepalakshmi]

I think I got what my teacher is saying.
I don't know if it make sense.
Since my state is pure, its fidelity should obey symmetry property i.e. $$F(\rho,\sigma)=F(\sigma,\rho) $$
so
$$|\langle\psi (\rho)|\psi (\sigma)|^2 = |\langle\psi (\sigma)|\psi (\rho)|^2$$
$$|\psi(\rho)\rangle = |\alpha\rangle |0\rangle$$
$$|\psi(\sigma)\rangle= |\alpha\cos(t)\rangle |i\alpha\sin(t)\rangle$$
therefore
$$|\langle\psi (\rho)|\psi (\sigma)|^2$$

$$=|(|\langle\alpha|\langle 0|)(|\cos(t)\alpha\rangle|i\alpha\sin(t)\rangle)|^2$$
$$= 1$$ (when t = 0)
similarly for
$$|\langle\psi (\sigma)|\psi (\rho)|^2$$
so I should get same fidelity irrespective of t

 

[deepalakshmi]

I think I got what my teacher is saying.
I don't know if it make sense.
Since my state is pure, its fidelity should obey symmetry property i.e. $$F(\rho,\sigma)=F(\sigma,\rho) $$
so
$$|\langle\psi (\rho)|\psi (\sigma)|^2 = |\langle\psi (\sigma)|\psi (\rho)|^2$$
$$|\psi(\rho)\rangle = |\alpha\rangle |0\rangle$$
$$|\psi(\sigma)\rangle= |\alpha\cos(t)\rangle |i\alpha\sin(t)\rangle$$
therefore
$$|\langle\psi (\rho)|\psi (\sigma)|^2$$

$$=|(|\langle\alpha|\langle 0|)(|\cos(t)\alpha\rangle|i\alpha\sin(t)\rangle)|^2$$
$$= 1$$ (when t = 0)
similarly for
$$|\langle\psi (\sigma)|\psi (\rho)|^2$$
so I should get same fidelity irrespective of t

I think it doesn't make sense

 

[deepalakshmi]

When will the pure state have constant fidelity?

 

[deepalakshmi]

Is there something wrong with my initial and final state?
"The fidelity between two states can be shown to never decrease when a non-selective quantum operation

is applied to the states" what does this mean and how is it related to my problem?

 

[deepalakshmi]

@Demystifier I am wrong. What my teacher meant was "At t = 90(degree), the fidelity is 0.00004 which is nearly equal to 0. But fidelity will be 0 only if the two states are orthogonal. But my case is not orthogonal. So he told me my calculation is wrong". I think it makes sense right?
Therefore something is wrong. But what is wrong?
My calculation for proving it is not orthogonal:
at t = 90(degree)
$$(\langle\alpha|\langle 0|)(|0\rangle|i\alpha\rangle)$$
$$\langle\alpha|0\rangle \langle 0|i\alpha\rangle$$
$$exp({-{|\alpha|}^2}{/2}) exp({-{|\alpha|}^2}{/2})$$
$$exp({-|\alpha|}^2)$$
But here if I substitute alpha as sqrt{5}
I am getting 0.006.
Then does it mean my state is orthogonal?( I am confused)

 

[Demystifier]

I am getting 0.006.

$0.006^2=0.000036\approx 0.00004$, which is the number your teacher gave. If you take my simplified expression in #4, you will see that the fidelity is really $e^{-2|\alpha|^2}$, which is $(e^{-|\alpha|^2})^2$.

Then does it mean my state is orthogonal?

No, it means that it's almost orthogonal.

 

[deepalakshmi]

At t=90(degree)
its inner product is approximately equal to 0.
Therefore its fidelity is 0 (approximately).
Is this statement correct?

 

[Demystifier]

At t=90(degree)
its inner product is approximately equal to 0.
Therefore its fidelity is 0 (approximately).
Is this statement correct?

Yes.

 

[deepalakshmi]

Yes.

But if take smaller values of alpha, I am not getting this statement. Why? For example; take alpha= sqrt{1}. Its inner product is 0.36 and fidelity is 0.1

 

[Demystifier]

But if take smaller values of alpha, I am not getting this statement. Why? For example; take alpha= sqrt{1}. Its inner product is 0.36 and fidelity is 0.1

What is the smallest positive number which is approximately equal to 0?

Maybe you also want to read this:
https://en.wikipedia.org/wiki/Sorites_paradox

 

[deepalakshmi]

@Demystifier
Now considering t = 30(degree)
$$|\psi\rangle=|\alpha\rangle|0\rangle$$
$$|\phi\rangle= |\cos(t)\alpha\rangle|i\alpha\sin(t)\rangle$$
$$= |(\sqrt{3}{/2})\alpha\rangle|(1{/2})i\alpha\rangle$$
$$F=|\sqrt{3}{/4}(|\langle\alpha|\langle 0|)(|\alpha\rangle|i\alpha\rangle)|^2$$
$$=|\sqrt{3}{/4}(|\langle\alpha|\alpha\rangle)(\langle 0|i\alpha\rangle)|^{2}$$
$$=3/16|e^{-\frac{|\alpha|^2}{2}}|^2$$
$$=(3/16)e^{-5}$$
$$=0.001$$

If I consider
$$F= e^{-2|\alpha|^2(1-\cos(t))}$$
$$=e^{-10(1-\sqrt{3}{/2})}$$
$$=0.26$$
Why there is a change in fidelity?

 

[Demystifier]

Why there is a change in fidelity?

You made an error again; $|c\alpha\rangle \neq c| \alpha\rangle$.

 

[deepalakshmi]

You made an error again; $|c\alpha\rangle \neq c| \alpha\rangle$.

Since C is just a value, can't I take it outside?

 

[deepalakshmi]

Then how should I find inner product of the state with value inside it?

 

[Demystifier]

Since C is just a value, can't I take it outside?

You can't. $\alpha$ is also just a value, why don't you take $\alpha$ outside instead? Think about it!

 

[Demystifier]

Then how should I find inner product of the state with value inside it?

The way you did it correctly in the first post.

 

[deepalakshmi]

$$F=|(\langle\alpha|\frac{\alpha\sqrt{3}}{2}\rangle)(\langle0|\frac{i\alpha}{2}\rangle)|^2$$

simplifying$$\langle\alpha|\frac{\sqrt{3}}{2}\alpha\rangle$$

$$=e^{-\frac{|\alpha|^2}{2}}\sum_{n=0}\frac{(\alpha^\ast)^n}{\sqrt{n!}}\langle n|e^{-\frac{|\alpha{\sqrt{3}{/2}}|^2}{2}}\sum_{m=0}\frac{(\alpha{\sqrt{3}{/2}})^m}{\sqrt{m!}}|m\rangle$$
$$
=e^{-\frac{|\alpha|^2}{2}}e^{-\frac{|\alpha{\sqrt{3}{/2}}|^2}{2}}e^{-\{(\sqrt{3}|\alpha|^2)/2)}
$$

Simplifying $$\langle 0|\frac{1}{2}i\alpha\rangle$$

$$=\langle 0| e^{-\frac{|i\alpha/2|^2}{2}}\sum_{n=0}e^{-\frac{|i\alpha/2|^2}{2}}\frac{(\alpha i{({1}{/2}}))^n}{\sqrt{n!}}|n\rangle$$

$$=e^{-\frac{|i\alpha/2|^2}{2}}$$

$$F=|e^{-\frac{|\alpha|^2}{2}}e^{-\frac{|\alpha{\sqrt{3}{/2}}|^2}{2}}e^{-\{(\sqrt{3}|\alpha|^2)/2)}e^{-\frac{|i\alpha/2|^2}{2}}|^2$$

 

[deepalakshmi]

While increasing the degree( 0,30,60,etc) fidelity keeps on decreasing and reaches 0 (1,0.2,0,0,0...). So can I conclude that overlapping of the two quantum state decreases while increasing the degree(time)?

 

[deepalakshmi]

This is graph which I got while plotting fidelity vs time. According to my graph, fidelity decreases and reaches 0 but again increases and decreases.

 

[deepalakshmi]

This is graph which I got while plotting fidelity vs time. According to my graph, fidelity decreases and reaches 0 but again increases and decreases.

From this graph what observations can be made?