Maximizing Roller Coaster Velocity and Height for a Safe Ride

[megaforcetkd]

Homework Statement

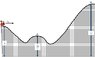
A frictionless roller coaster is given an initial velocity of vo at a height of h = 85 m, as in figure shown. The radius of curvature of the track at point A is 127 m.

(a) Find the maximum value of vo so that the roller coaster stays on the track at point A solely because of gravity.

(b) Using the value of vo calculated in part (a), determine the value of h' that is necessary if the roller coaster just makes it to point B.

(c) What condition must the radius of curvature be in relation to the height h for this problem to work? Show all work leading to your conclusion.

Homework Equations

Fn = Fg
MEi = MEf
1/2mv1^2 + mgh1 = 1/2mv2^2 + mgh2

The Attempt at a Solution

I don't know how to approach this at all... Never done anything like this.

 

[megaforcetkd]

guys this is reallly driving me mad =/ i can't figure this out at all!

 

[cristo]

You must show some work, or some effort before we can help you. Also, note that your image has not been approved yet: have patience! Perhaps someone will help when this has been approved.

 

[megaforcetkd]

I know that but in this problem I really have no idea where to go with it.. I thought I could use the normal force and set that to 0 and do sum of forces but I can't do that since there's no mass to cancel out I think... And what does the problem mean when it says the radius of the curvature?

 

[Doc Al]

I know that but in this problem I really have no idea where to go with it.. I thought I could use the normal force and set that to 0 and do sum of forces but I can't do that since there's no mass to cancel out I think...

You are heading in the right direction. Just call the mass "m" and see what happens.

And what does the problem mean when it says the radius of the curvature?

It means that they are giving you a big hint that the car must execute circular motion when going over that hill. What kind of acceleration is it undergoing? Apply Newton's 2nd law.

 

[megaforcetkd]

ahhh ok i figured out part A but for some reason i can't do B...

for part a i just use MAc = MG and solved for v, then used MEi = MEf an plugged that v into the equation V = sqrt(gR) and i found Vo..

Vo = 26.26 m/s or 94.54 km/h

For part B i tried doing

mg (delta)h = .5mv1^2
delta h = .5 v1^2 / g

i got 35.18m, and added 127 (radius) to that, but got the wrong answer... any help please?

 

[Doc Al]

For part B i tried doing

mg (delta)h = .5mv1^2
delta h = .5 v1^2 / g

i got 35.18m, and added 127 (radius) to that, but got the wrong answer... any help please?

Not quite sure what you're doing here. You have the total energy at the starting point, equate that the to the final energy at point B.

 

[megaforcetkd]

ok i tried doing...

.5mVo^2 + mgh1 = mgh3

i got that number smaller than my initial height?

 

[Doc Al]

Given that equation, how can h3 < h1?