Measuring distance between two stars in a binary system

[TheCelt]

Hello

I am trying to teach myself some basic maths for astronomy from a book, namely trying to calculate the distance between two stars in a binary system.

One thing i am confused with is what angular separation means and how it can be translated to true physical distance between them using trigonometry. I am trying to visualise it but its a bit confusing at the moment. The book did not explain it as it seems to have presumed i already understood this.

Firstly what does it mean for each star to have an angular separation from centre of mass, eg if star A has 5 arcsec and star B has 10 arcsec what are these angles relative to? And if you know the distance D of the system from Earth, i presume trigonometry can be done to solve it but i am struggling to visualise how to draw it out to do the trigonometry for it at the moment.

I made a drawing to show the setup of what i think it might mean:

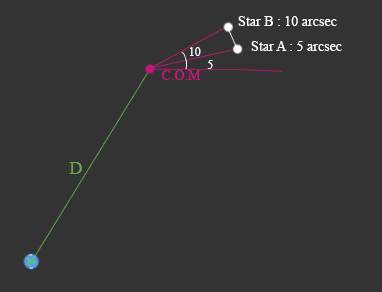
When they say angular separation from COM is this correct thinking? If so how are they defining the angle? What constitutes the 0 arcsec line, what counts as the positive x-axis in space i guess is what I am asking.

Secondly from that i do not understand how you might calculate the physical separation distance between the two stars (white line magnitude). Mainly because i am confused by the angle situation.

 

[Halc]

CoM has to be between the two stars of a binary pair, but probably not half way.
So the angle for each is going to be the deviation from that point. The line from you to the CoM is the arcsec line. A star with half the mass of the other will have twice the angular separation at any given moment, but the angular separation between the stars will change over the course of their orbit, possibly dropping to zero if you're on their orbital plane. The physical distance between them will also be changing as orbits are rarely perfectly circular.

Distance from you to the binary pair isn't trivial to figure out. Usually for something nearby, parallax is used to measure distances, but it only works so far.

 

[TheCelt]

CoM has to be between the two stars of a binary pair, but probably not half way.
So the angle for each is going to be the deviation from that point. The line from you to the CoM is the arcsec line. A star with half the mass of the other will have twice the angular separation at any given moment, but the angular separation between the stars will change over the course of their orbit, possibly dropping to zero if you're on their orbital plane. The physical distance between them will also be changing as orbits are rarely perfectly circular.

Distance from you to the binary pair isn't trivial to figure out. Usually for something nearby, parallax is used to measure distances, but it only works so far.

Thanks for the reply, the bit i am struggling with is how to draw the triangle as a diagram so i can understand the trig used to calculate it.

I refer to this question in my book which during the calculations it finds the separation of two stars (which is what i am trying to solve) and it uses tangent and multiplies it by the distance from Earth. But i can't visualise the triangle to understand why they use tangent or why multiply by the distance from Earth.

I also don't understand how that gives the distance from the center of mass.

 

[Halc]

The text there spells out the triangle pretty clearly: Earth, CoM, star1 is one triangle, Earth, CoM, star2 is the other. You know the length of one side (1.31 pc) so the tangent(measured angle) gives you the other (distance to star from CoM). The mass ratio here is about 6 to 5 respectively between the stars.

The text seems to indicate that the angular separation is constant, which is really rare. Maybe they mean the max angular separation, which gives a distance between the stars when they're equidistant from Earth.

Given their separation distance and orbital period, their respective masses can be computed.

 

[TheCelt]

Well the book simplifies things since its only introducing the subject and hasn't added the complexity of things moving.

I think i understand how to visualise it now but i think my trig is wrong because i seem to find using the sin function is required not the tan function, so i don't quite see why they use tan, unless i am still drawing it wrong?

 

[PeroK]

You've still not got the COM on a straight line between the stars. Your right angles are in the wrong place, hence the confusion between sine and tangent.

 

[PeroK]

Well the book simplifies things since its only introducing the subject and hasn't added the complexity of things moving.

If the stars are orbiting each other then they are moving!

 

[TheCelt]

You've still not got the COM on a straight line between the stars. Your right angles are in the wrong place, hence the confusion between sine and tangent.

Well I couldn't visually work out how to draw it properly as I have said, i was not sure where the right angle would be, and its not clear to my why there would be one (see picture 2). I don't see why we draw them at right angle to the COM relative to the vector from Earth. Because after some time won't be they will be shifted slightly since as you mention - they are moving...

You seem to be saying the right angles go here like this:

But what if it's another moment in time since they are moving why wouldn't it be like this image below having no right angles at all?

Doesn't really make much sense to me why we include a right angle by default because i don't see a right angle in the second diagram.

 

[PeroK]

That's why @Halc pointed out that we must be talking about the maximum angular separation.

The text seems to indicate that the angular separation is constant, which is really rare. Maybe they mean the max angular separation, which gives a distance between the stars when they're equidistant from Earth.

The maximum occurs when you have the right-angles at the COM in your diagram.

 

[Halc]

The maximum occurs when you have the right-angles at the COM in your diagram.

Not necessarily I think. It is true for a reasonably circular orbit. There are clues to computing actual orientations of orbits and thus maximum distances when the orbit is highly elliptical.
Take some of the stars orbiting Sgr-A:

I see S1 as a fairly circular orbit, despite S13 appearing to be more circular.
S8 has its minor axis (and possibly its major axis, hard to tell) nearly perpendicular to our field of view, so its maximum angular separation is actually a good measure of its actual distance.
S6, S14 and S27 are good examples where this is not the case. We're looking at their orbits fairly edge-on and the angle with our line of sight when these stars are at maximum angular separation is anything but a right angle.
S17 I think is the most circular of all of these, despite it appearing highly eccentric from our PoV. The angles here would be closer to right angles at points of maximum angular separation.

 

[Buzz Bloom]

What does the acronym "CoM" stand for?

ADDED
Now I got it: Center of Mass.