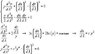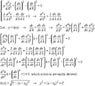Methods for Solving Non-Linear Second Order Systems of Differential Equations

[LAHLH]

Hi,

could anyone tell me what methods I would need to solve this system:

y\frac{d^2 y}{d\lambda^2}+\left(\frac{dx}{d\lambda}\right)^2-\left(\frac{dy}{d\lambda}\right)^2=0

\frac{y}{2}\frac{d^2x}{d \lambda ^2}-\left(\frac{dx}{d\lambda}\right)\left(\frac{dy}{d\lambda}\right)=0

I believe the solution is (x-x_0)^2+y^2=l^2

I think (unless I've made a mistake anyway) that these are the geodesic equations for H^2, so the solutions are semicircles in the upper half plane (cf Sean Carroll). I'm not sure how to solve these however despite him saying "it is straightforward to show...", because they seem to be non linear and second order.

Thanks

 

[LAHLH]

I've managed to solve the second equation using integrating factor methods.

If we write u=\frac{dx}{d\lambda} then the second equation is:

\frac{du}{d\lambda}+\left[-\frac{2}{y}\left(\frac{dy}{d\lambda}\right)\right] u=0

So now this is of the form u' (\lambda)+P(\lambda) u(\lambda) =0 and we can use int factors. Which we can find as M(\lambda)=exp\left[\int -\frac{2}{y}\left(\frac{dy}{d\lambda}\right) d\lambda\right]=\frac{1}{y^2}

So multiplying our equation by this leads to:

\frac{1}{y^2}\frac{du}{d\lambda}-\frac{2}{y^3}\left(\frac{dy}{d\lambda}\right) u=0

or

\frac{d}{d\lambda} \left[\frac{1}{y^2} u\right] =0

from which we find u=\frac{1}{C} y^2

So now we have \frac{dx}{d\lambda}=\frac{1}{C} y^2 we can plug this in equation one to obtain:

\frac{d^2 y}{d\lambda^2}-\frac{1}{y}\left(\frac{dy}{d\lambda}\right)^2+\frac{y^3}{C^2}=0

So now I just need to solve this second order non linear equation.

 

[jackmell]

I'm not sure how to solve these however despite him saying "it is straightforward to show...", because they seem to be non linear and second order.

Thanks

You sure that doesn't mean, "it is straightforward to show that this solution solves the system?"

If so, then you can take the solution:

(x-x_0)^2+y^2=a^2

differentiate once and twice, solve for x' and x'', back-substitute into the second equation, then by using the first equation show the second equation is zero and thereby show the solution satisfies the second equation. And I assume you can do likewise for the first and therefore show it's pretty straightforward to show that solution satisfies the system.

 

[LAHLH]

You sure that doesn't mean, "it is straightforward to show that this solution solves the system?"

If so, then you can take the solution:

(x-x_0)^2+y^2=a^2

differentiate once and twice, solve for x' and x'', back-substitute into the second equation, then by using the first equation show the second equation is zero and thereby show the solution satisfies the second equation. And I assume you can do likewise for the first and therefore show it's pretty straightforward to show that solution satisfies the system.

you are probably correct that he did mean just do this I suppose. I guess now I've come this far I'd like to solve it explicitely however. I think it should be do able despite it being non linear, as their is no lambda factors, y'' is just a function of y' and y

 

[Matthew Rodman]

Your second-order equation

y^{\prime \prime} - \frac{y^{\prime 2}}{y} + \frac{y^3}{C^2} = 0

probably has many solutions, but there is a simple solution of the form

y(\lambda) = \pm i \alpha C \sec{(\alpha \lambda + \beta)}

where \alpha and \beta are constants. You can show this very easily by substitution of a trial solution of the form

y(\lambda) = A \sec{(\alpha \lambda + \beta)}.

 

[JJacquelin]

Another way to solve it. Simpler on my opinion.
The first part is presented in attachment.
The ODE obtained isn't very difficult to be solved. I have not enough time this evening to write it up. Next part for tomorrow.

 

[jackmell]

Another way to solve it. Simpler on my opinion.
The first part is presented in attachment.
The ODE obtained isn't very difficult to be solved. I have not enough time this evening to write it up. Next part for tomorrow.

Man that is so slick. :)

So then we get:

yy''+c^2y^4-\left(y'\right)^2=0

Don't know what Jacquelin has in mind but I would then let p=y' and obtain:

yp\frac{dp}{dy}+c^2y^4-p^2=0

or:

(c^2y^4-p^2)dy+(yp)dp=0

for which I think an integrating factor is \frac{1}{y^3}[/tex] which will then make the equation exact and we can solve it using that method.

 

[JJacquelin]

The method proposed by jackmell would probably solve the EDO.
My method is not exactly the same, but the result is obtained anyway.

 

[JJacquelin]

If we are not interested to explicitly know x and y as function of lambda, but if we only are interested to know the relationship between x and y, then a much simpler method is possible :

 

[LAHLH]

These are great thanks alot. I must be being stupid, and I follow both your arguments upto the last line, but I can't quite see how to solve your final equations with integrating factors, e.g. for \frac{d^2h}{dx^2}+\frac{1}{h}\left(\frac{dh}{dx}\right)^2+\frac{1}{h}=0 how does one procede?

I assumed from here you would need to make a substitution p=h' which leads me to h''=\frac{dh}{dx}=\frac{dp}{dh}\frac{dh}{dx}=pp' so
pp'h+p^2+1=0 but this isn't the standard form I'm used to for finding integrating factors.

EDIT: actually is it just seperable?

 

[JJacquelin]

Just note that h*h''+(h')² = (h*h')'
(h*h')' = -1
h*h' = -x+x_0
etc.

In fact, what is done in my preceeding post is only to eliminate lambda from the two primary ODE.