mathmari
Gold Member
MHB
- 4,984
- 7
Hey! 
I am looking the following:
Determine a disjunctive normal form for the expression $$x_1\left (\left (x_2x_3\lor \bar{x}_2x_4\right )\lor x_2\lor x_3x_4\right )\lor x_2\bar{x}_4\bar{\left (\bar{x}_1x_3\right )}\lor x_1x_3\bar{x}_4$$ and minimize it using a Karnaugh Diagram.
The above expression is equivalent to $$ x_1x_2x_3\lor x_1\bar{x}_2x_4\lor x_1x_2\bar{x}_3x_4\lor x_2\bar{x}_4x_1\lor x_2\bar{x}_4\bar{x}_3\lor x_1x_3\bar{x}_4$$
Does each term has t contain all the variables? If yes, then if one variable is missing then we replace that by $x_i\lor \bar{x}_i$.
If we have to do that in that way and we simplify the expression and so we get: $$x_1x_2x_3x_4\lor x_1x_2x_3\bar{x}_4\lor x_1\bar{x}_2x_3x_4\lor x_1\bar{x}_2\bar{x}_3x_4\lor x_1x_1\bar{x}_3x_4\lor x_1x_2\bar{x}_3\bar{x}_4\lor \bar{x}_1x_2\bar{x}_3\bar{x}_4\lor x_1\bar{x}_2x_3\bar{x}_4$$
Is this a disjunctive normal form that we arelooking for? (Wondering)
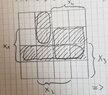
To create the Karnaugh Diagram, is the form of that diagram always the same? I mean how we name the edges $x_1, x_2, x_3, x_4$, as for example:
View attachment 9007
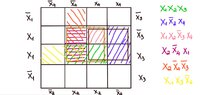
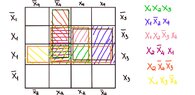
To fill that diagramm do we need the expression to contain all the variables? I mean could we do that if we have the above expression in the form $$ x_1x_2x_3\lor x_1\bar{x}_2x_4\lor x_1x_2\bar{x}_3x_4\lor x_2\bar{x}_4x_1\lor x_2\bar{x}_4\bar{x}_3\lor x_1x_3\bar{x}_4$$ ? (Wondering)
Could you explain to me that method? After filling that table how can we continue to determine the minimal expression? (Wondering)
I am looking the following:
Determine a disjunctive normal form for the expression $$x_1\left (\left (x_2x_3\lor \bar{x}_2x_4\right )\lor x_2\lor x_3x_4\right )\lor x_2\bar{x}_4\bar{\left (\bar{x}_1x_3\right )}\lor x_1x_3\bar{x}_4$$ and minimize it using a Karnaugh Diagram.
The above expression is equivalent to $$ x_1x_2x_3\lor x_1\bar{x}_2x_4\lor x_1x_2\bar{x}_3x_4\lor x_2\bar{x}_4x_1\lor x_2\bar{x}_4\bar{x}_3\lor x_1x_3\bar{x}_4$$
Does each term has t contain all the variables? If yes, then if one variable is missing then we replace that by $x_i\lor \bar{x}_i$.
If we have to do that in that way and we simplify the expression and so we get: $$x_1x_2x_3x_4\lor x_1x_2x_3\bar{x}_4\lor x_1\bar{x}_2x_3x_4\lor x_1\bar{x}_2\bar{x}_3x_4\lor x_1x_1\bar{x}_3x_4\lor x_1x_2\bar{x}_3\bar{x}_4\lor \bar{x}_1x_2\bar{x}_3\bar{x}_4\lor x_1\bar{x}_2x_3\bar{x}_4$$
Is this a disjunctive normal form that we arelooking for? (Wondering)
To create the Karnaugh Diagram, is the form of that diagram always the same? I mean how we name the edges $x_1, x_2, x_3, x_4$, as for example:
View attachment 9007
To fill that diagramm do we need the expression to contain all the variables? I mean could we do that if we have the above expression in the form $$ x_1x_2x_3\lor x_1\bar{x}_2x_4\lor x_1x_2\bar{x}_3x_4\lor x_2\bar{x}_4x_1\lor x_2\bar{x}_4\bar{x}_3\lor x_1x_3\bar{x}_4$$ ? (Wondering)
Could you explain to me that method? After filling that table how can we continue to determine the minimal expression? (Wondering)