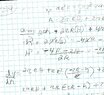leprofece
- 239
- 0
279) A body is formed by a straight circular cylinder which ends up in a hemisphere. What are the dimensions that should have this body so the total surface area is minimal, if your volume is
answer Cubic sqrt( 3V/5 pi)
i tried to post an image of my notes and i couldnot i will type later
Vt = pir2H +2/3piR2 constant
A= 2pirH+ 2pir2
Derive implicit 2piH + pir(dH) + 4pir
dh = (-2r-h)/(r)
derive volume 2pirH + pir2(dH) + 2pir2
2pirH + pir2(-2r-h) + 2pir2 = 0
And I got piRh = 0
So h = 0 and this is not the answer
answer Cubic sqrt( 3V/5 pi)
i tried to post an image of my notes and i couldnot i will type later
Vt = pir2H +2/3piR2 constant
A= 2pirH+ 2pir2
Derive implicit 2piH + pir(dH) + 4pir
dh = (-2r-h)/(r)
derive volume 2pirH + pir2(dH) + 2pir2
2pirH + pir2(-2r-h) + 2pir2 = 0
And I got piRh = 0
So h = 0 and this is not the answer
Last edited: