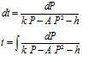Discussion Overview
The discussion revolves around solving the differential equation dP/dt = k P - A P² - h, focusing on the mathematical techniques required for integration and manipulation of the equation. The scope includes mathematical reasoning and potential applications of the model.
Discussion Character
- Mathematical reasoning, Homework-related
Main Points Raised
- One participant, NZBRU, seeks assistance in solving the equation, indicating familiarity with partial fractions and a previous solution to a related equation.
- Another participant provides a transformation of the equation, suggesting a method involving integration and a substitution for simplification.
- A follow-up post questions the correctness of the transformation and integration steps, indicating uncertainty about the notation used.
- A later reply mentions that integration leads to a function t(P), implying that an inverse function P(t) can be derived.
Areas of Agreement / Disagreement
The discussion contains multiple competing views on the integration process and notation, with no consensus reached on the correct approach or final form of the solution.
Contextual Notes
Participants express uncertainty regarding the notation and integration steps, highlighting potential limitations in understanding the transformations applied to the equation.