WMDhamnekar
MHB
- 378
- 30
Hello,
The sigma $(\sigma)$ molecular orbitals are symmetrical around the bond-axis while pi $(\pi)$ molecular orbitals are not symmetrical. For example, the linear combination of 1s orbitals centered on two nuclei produces two molecular orbitals which are symmetrical around the bond-axis. Such molecular orbitals are of the $\sigma$ type and are designated as $\sigma1s$ and $\sigma^*1s$ [Fig. 4.20(a)].
If internuclear axis is taken to be in the z-direction, it can be seen that a linear combination of $2p_z$ - orbitals of two atoms also produces two sigma molecular orbitals designated as $\sigma 2p_z$ and $\sigma^*2p_z .$ [Fig. 4.20(b)]
Molecular orbitals obtained from $2p_x$ and $2p_y$ orbitals are not symmetrical around the bond axis because of the presence of positive lobes above and negative lobes below the molecular plane. Such molecular orbitals, are labelled as $\pi$ and $\pi^*$ [Fig. 4.20(c)].
A $\pi$ bonding MO has larger electron density above and below the inter -nuclear axis. The $\pi^*$ antibonding MO has a node between the nuclei.
I want explanations about the enclosed areas in the following energy diagram.
In 1s orbital of two atoms, what does +and dot represent?
In $2p_z$ and $2p_x$ orbitals of two atoms, what does +,-, and dot between them represent?
Why 1s orbital doesn't have -(minus) sign along with + and dot symbols?
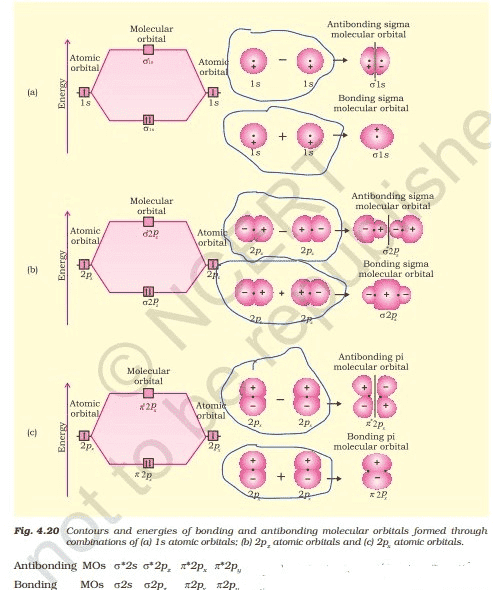
The sigma $(\sigma)$ molecular orbitals are symmetrical around the bond-axis while pi $(\pi)$ molecular orbitals are not symmetrical. For example, the linear combination of 1s orbitals centered on two nuclei produces two molecular orbitals which are symmetrical around the bond-axis. Such molecular orbitals are of the $\sigma$ type and are designated as $\sigma1s$ and $\sigma^*1s$ [Fig. 4.20(a)].
If internuclear axis is taken to be in the z-direction, it can be seen that a linear combination of $2p_z$ - orbitals of two atoms also produces two sigma molecular orbitals designated as $\sigma 2p_z$ and $\sigma^*2p_z .$ [Fig. 4.20(b)]
Molecular orbitals obtained from $2p_x$ and $2p_y$ orbitals are not symmetrical around the bond axis because of the presence of positive lobes above and negative lobes below the molecular plane. Such molecular orbitals, are labelled as $\pi$ and $\pi^*$ [Fig. 4.20(c)].
A $\pi$ bonding MO has larger electron density above and below the inter -nuclear axis. The $\pi^*$ antibonding MO has a node between the nuclei.
I want explanations about the enclosed areas in the following energy diagram.
In 1s orbital of two atoms, what does +and dot represent?
In $2p_z$ and $2p_x$ orbitals of two atoms, what does +,-, and dot between them represent?
Why 1s orbital doesn't have -(minus) sign along with + and dot symbols?