Moment Analysis: Sign Conventions & Force Selection

[aahas3]

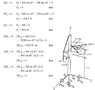
I'm having trouble determining the sign conventions for the appropriate moments and which forces correspond to the appropriate moment analysis in the following question .The solutions are provided but i still need to know the fundamentals behind such selection and the sign conventions for it as the demonstrator explained how to use the right hand screw rule I am not really sure.

Egs When applying Fz = 400 how do we know the moment is positive giving 400*0.1 and the two right angle forces of 300. Their X components how do we discern whether their positive or negative when doing the moment equations.

Last how to know which forces should be used to determine the moment for the individual moment cases ies ƩMx or ƩMy. Thnks

 

[SteamKing]

Aside from the obvious defects in this problem (Forces given in lbs in the text, Forces on diagram are in Newtons; neither of which convert), for 3-D statics, assume that for forces and distances, positive magnitudes correspond to positive directions as indicated by the coordinate axes.

To derive the corresponding moment direction, one can always fall back on the definition of the cross-product for two vectors. For example, say we use a radius of 1 m (i-cap) and a force of 1 N (j-cap). What would be the direction of the resulting moment?

Setting up the cross product determinant:

| i   j   k |
| 1   0   0 |  =  (0 i  +  0 j  + 1 k) N-m
| 0   1   0 |

This is one way of determining a positive sense for a moment.

Another simpler method is to write out the unit vectors thus:

i j k | i j

This is a memory device to help one understand the cross product of the individual unit vectors.

For example, i x j = k, which we can see by looking at the first two unit vectors, i and j, and then reading the next unit vector, k. If we continue, working from left to right, we obtain the following results:

i x j = k
j x k = i
k x i = j

If we were to start at the extreme right and work back to the left, then three different results are obtained:

j x i = -k
i x k = -j
k x j = -i

In the case of the moment produced by the 400 N tension, the solution has cheated a little and not included the proper signs of the tension and the moment arm of 0.9 m. In both instances, the magnitudes should have been negative, but the solution writer got lazy and omitted them. Thus the proper calculation should have been

r = -0.9 m (j-cap)
F = -400 N (k-cap)

moment = r x F = -0.9 j x -400 k = 360 N-m i

which matches the diagram.

By using these methods to compute the moments, much worry is avoided in trying to figure out about which axis the moment will be produced.

For more about cross products see :

https://ecourses.ou.edu/cgi-bin/ebook.cgi?doc=&topic=st&chap_sec=04.3&page=theory