Moment of inertia and torque of a yoyo

[JulienB]

Homework Statement

Hi everybody! I know that is a classical problem, but I haven't been able to find an answer to my questions in the other threads so here we go:

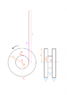
We have a yoyo made of 3 aluminium disks (density ρ). The two side disks have a radius R and thickness D, and the middle disk has a radius R₀ and a thickness D₀. The string has length l (see picture).

a) Calculate the moment of inertia of the yoyo. Derive then the moment of inertia of a disk of mass M and radius r about its axis of symmetry.
b) Calculate the torque when the yoyo is "falling". In which direction does it point?
c) What is the angular frequency ω when the string is half unrolled?

Homework Equations

Moment of inertia, torque, tangential acceleration and so on.

The Attempt at a Solution

a) My first issue attempting to solve this problem is that I am unsure whether the radius R₀ should be considered when calculating the moment of inertia of the yoyo. I am confused, because the string is responsible for the rotation but yet the yoyo is rotating about its axis of symmetry. Therefore I would assume the moment of inertia of the yoyo is:

I_yoyo = 2⋅I_{big disk} + I_{small disk}
= 2⋅(ρπDR⁴) + ½ρπD₀R₀⁴
= ρπ⋅(DR⁴ + ½⋅D₀R₀⁴)

I quickly add the calculation for the moment of inertia of a disk:
I_disk = ρ∫ r²dV = ρDπr⁴/2 = ½ ⋅Mr²

Is that correct, or is there any need to use the parallel axis theorem?

b) Here it becomes complicated. I think the only force playing a role on the rotation is the tension force of the string, therefore:

Στ = I⋅α = F⋅R₀ where α is of course the angular acceleration ⇒ α = a_T/R₀.

I also think a_T = a_y and M_yoyo⋅g - I⋅α/R₀ = M_yoyo⋅g - I⋅a_y/R₀² = M_yoyo⋅a_y

⇒ a_y = M_yoyo⋅g / (M_yoyo + I/R₀)

But when I insert that in my torque equation, it gets crazy:

Στ = I⋅α = (I/r₀)⋅(M_yoyo⋅g / M + I/R₀)

When I plug my moment of inertia in, nothing good comes out and it gets very messy. Have I made a mistake or should I also put up an equation of energy?Thank you very much in advance.EDIT: I just saw a similar problem on internet where the guy takes the point of contact of the string with the disk as the torque axis. Is that really allowed?? If so, would I have to use the parallel axis theorem because we don't take the center of the yoyo as axis of rotation anymore? Julien.

 

[haruspex]

You seem to have forgotten the factor 1/2 in I_{big disk}.
You can approach it in either of two ways. Use the MoI about mass centre and torque about mass centre (radius x tension); or use the parallel axis theorem to find the MoI about point of contact of the string and torque about that point (radius x mg). They should lead to the same answer. You just have to pick your axis and be consistent.

 

[JulienB]

@haruspex I don't think I forgot the 1/2, because there are two big disks. No? I'll give the problem another try tomorrow and post again :)

 

[haruspex]

@haruspex I don't think I forgot the 1/2, because there are two big disks. No? I'll give the problem another try tomorrow and post again :)

Well, you forgot it here:

= 2⋅(ρπDR4) + ½ρπD₀R₀⁴

But I see you found it again here:

= ρπ⋅(DR4 + ½⋅D₀R₀⁴)

 

[JulienB]

@haruspex My mistake I forgot it by copying my notes. Thank you for your attention :)

 

[JulienB]

I gave it another go but still get a crazy result for the torque:

 

[haruspex]

I gave it another go but still get a crazy result for the torque:

Why do you think it's crazy. I would not bother multiplying out the factors in the numerator. You have an error in the denominator going from the second line to the third line... a factor of 2.

 

[JulienB]

@haruspex Thank you for your answer. I'm doing the problem again, and I'm wondering: shouldn't I have taken a_T = g (instead of the whole acceleration (m⋅g - T)/m) in my torque equation?

Julien.

 

[haruspex]

@haruspex Thank you for your answer. I'm doing the problem again, and I'm wondering: shouldn't I have taken a_T = g (instead of the whole acceleration (m⋅g - T)/m) in my torque equation?

Julien.

How are you defining a_T? Certainly the sum of vertical forces is mg-T downwards.

 

[JulienB]

@haruspex Nevermind I got it wrong. Sorry for that :)