Moment of Inertia for three rods

[hL]

I'm having some problems doing my homework. Please help me.

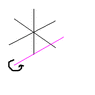
1. Three rods, each of length L and mass M, are welded together perpendicularly (like an x-y-z coordinate system). The axis of rotation is drawn in pink in the image below. I have to find the moment of inertia.

I used the parallel-axis theorem to get:
I = I-cm + MD²
I = 2(.5ML²) + M(L/2)²
I = (5/4)ML²

I'm not sure if I'm right, could someone check my method?

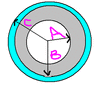
2. Picture 2 is a car tire. It has two sidewalls (gray) of uniform thickness 0.635 cm and a tread wall (cyan) of uniform thickness 2.5 cm and width 20.0 cm. Its density is uniform, with a value of 1.10E3 kg. Find its moment of inertia about an axis through its center, perpendicular to the plane of the sidewalls. (A = 16.5 cm, B = 30.5 cm, C = 33.0 cm).

I have no idea what to do.

3. What values would you need to estimate the moment of inertia of your body as you stand tall and turn in a vertical axis passing through the top of your head to the point between your feet?

Again, I have no idea what to do.

Thanks in advance.

 

[Sirus]

For all three problems, you need to split objects of compound shapes (i.e. of shapes compiled from many simpler shapes) into their familiar parts, of which you know the equations for moment of inertia. For #1, you must find the moment of inertia of each rod with respect to the axis of rotation, then add them together. For #2, what familiar shapes make up the tire? For #3, what shape is similar to the human body?

 

[wais]

1. Your method for finding the moment of inertia for the three rods seems correct. You used the parallel-axis theorem to find the moment of inertia for each rod and then added them together. However, it would be helpful if you could provide a diagram or image of the setup to confirm your calculation.

2. For the car tire problem, you can use the formula for moment of inertia of a cylinder, I = (1/2)MR², where M is the mass of the cylinder and R is the radius of the cylinder. In this case, the cylinder is made up of two sidewalls and a tread wall. You can find the mass of the cylinder by finding the volume and then multiplying it by the density. The volume can be calculated by finding the volume of each individual component (sidewalls and tread wall) and then adding them together. Once you have the mass and radius of the cylinder, you can plug them into the formula to find the moment of inertia.

3. To estimate the moment of inertia of your body, you would need to know your mass and the distance from the axis of rotation (vertical axis passing through the top of your head) to your center of mass. You can estimate your mass using your body weight, and for the distance, you can measure it or estimate it based on your body proportions. Once you have these values, you can use the formula for moment of inertia of a point mass, I = MR², where M is your mass and R is the distance from the axis of rotation to your center of mass.