darkdave3000
- 242
- 5
Why do these properties each have a range each instead of a fixed value? Is it because of the 8 year precession?
I'm writing a graphical software that will illustrate the lunar orbit. I planned to show the precession too but am unsure what values of apogee and perigee and even eccentricity because of the ranges given in Wikipedia.
Note the fixed values that are given are given as averages of the given ranges. Once again, why are there ranges?
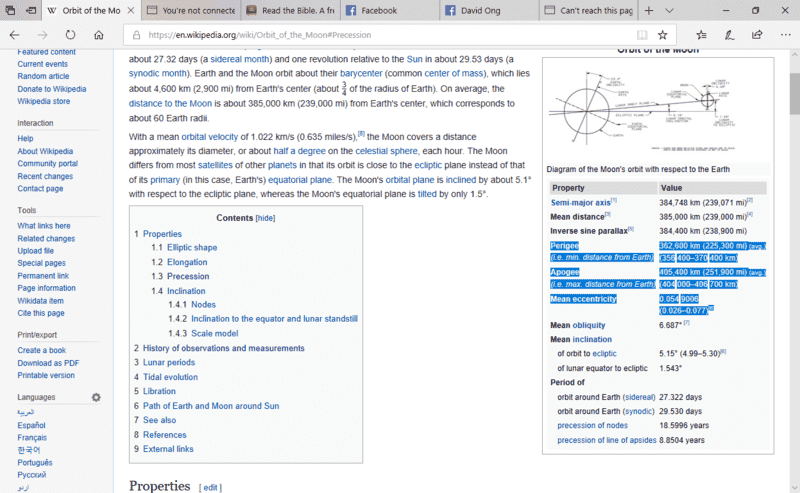
I'm writing a graphical software that will illustrate the lunar orbit. I planned to show the precession too but am unsure what values of apogee and perigee and even eccentricity because of the ranges given in Wikipedia.
Note the fixed values that are given are given as averages of the given ranges. Once again, why are there ranges?