SUMMARY
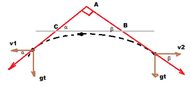
Two particles in a uniform gravitational field with acceleration \(g\) move horizontally with initial velocities \(v_1 = 3 \text{ms}^{-1}\) and \(v_2 = 4 \text{ms}^{-1}\) in opposite directions. The distance between the particles when their velocities become mutually perpendicular is calculated using the time \(t\) derived from the equation \(t = \frac{\sqrt{v_1 v_2}}{g}\). The total separation is given by \((v_1 + v_2) \frac{\sqrt{v_1 v_2}}{g}\), resulting in a final expression for distance as \(7t\) m when the vertical component of velocity reaches \(2\sqrt{3}\) m/s.
PREREQUISITES
- Understanding of kinematics in a uniform gravitational field
- Familiarity with vector components of velocity
- Knowledge of the dot product and its application in determining perpendicular vectors
- Basic algebra for solving equations of motion
NEXT STEPS
- Study the principles of projectile motion in uniform gravitational fields
- Learn about vector decomposition and its applications in physics
- Explore the concept of relative velocity in two-dimensional motion
- Investigate advanced kinematic equations and their derivations
USEFUL FOR
Students of physics, educators teaching mechanics, and anyone interested in understanding the dynamics of particles in gravitational fields.