re444
- 14
- 0
Hi everybody,
I need to solve a 1st order PDE for my thesis and I'm not a specialist in this field.
I've read some texts about this and know one method of solving a 1st order PDE is the method of characteristics. since my equation is nonlinear and a bit complicated, I'm going to solve it numerically.
Equation should be solved in x-z domain so I have to solve a system of five ODEs and is a boundary problem (Cauchy problem). According to the text found in internet the five are of the form:
main formula:

ODEs to be solved:
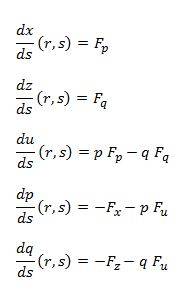
I omit the 5 boundary equations which are of the form for example for q, q(r,0)=g(r).
In the case of analytical solution at the end, u, the answer, will become: u=u(x,z). But when trying to solve numerically I'm a bit confused. How I should treat the parameter 'r' in ODEs? Software s like Matlab solves system of ODEs but this kind of ODEs with two parameters, 'r' and 's', seems strange to me!
Any suggestion and hint is really appreciated,
Reza,
I need to solve a 1st order PDE for my thesis and I'm not a specialist in this field.
I've read some texts about this and know one method of solving a 1st order PDE is the method of characteristics. since my equation is nonlinear and a bit complicated, I'm going to solve it numerically.
Equation should be solved in x-z domain so I have to solve a system of five ODEs and is a boundary problem (Cauchy problem). According to the text found in internet the five are of the form:
main formula:
ODEs to be solved:
I omit the 5 boundary equations which are of the form for example for q, q(r,0)=g(r).
In the case of analytical solution at the end, u, the answer, will become: u=u(x,z). But when trying to solve numerically I'm a bit confused. How I should treat the parameter 'r' in ODEs? Software s like Matlab solves system of ODEs but this kind of ODEs with two parameters, 'r' and 's', seems strange to me!
Any suggestion and hint is really appreciated,
Reza,