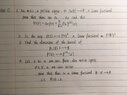Need some hints on my HW about Linear functionals

[BaconInDistress]

I not very good at using the LaTex editor, so I took a photo of my HW questions.
View attachment 8831
For the first question, I'm not really sure how to get started, should I write out a specific case? Like what would $$\varphi (P)$$ be when m=1?

For the second question, I know that a linear functional have two properties, one being $$\varphi(u +v) = \varphi(u) + \varphi(v)$$ and the other one being $$\varphi(\lambda u) = \lambda\varphi(u)$$. I'm a bit confused about the mapping, is it saying that when we have a polynomial P(z), the map makes it goes to p(0) for all z?

 

[Evgeny.Makarov]

Perhaps you should start by defining notations, including $\mathbb{F}$, $P_m(\mathbb{F})$ and $p^{(k)}(x)$. Also, it is not very clear which of $p$'s are uppercase and which are lowercase letters. For example, in problem 1 in the left-hand side $\varphi(P)$ the letter $P$ seems to be uppercase, but in the right-hand side it is probably lowercase.

 

[BaconInDistress]

According to the textbook we use, $$F$$ is a field over $$\Bbb{R}$$ or $$\Bbb{C}$$. $${P}_{m}(F)$$ is the polynomial space of degree m.
One of the many problem with my homework is indeed the handwriting, my professor is not very consistent with his upper and lower case letters. I just copied down what he wrote.
I think for question one, we need to prove the existence of constants $${a}_{0},...,{a}_{m}$$ such that the linear functional $$\varphi (P) = {a}_{0}p(0) + \sum_{k=1}^{m} {p}^{(k)}(0)$$
Not really sure how to go from there

 

[Evgeny.Makarov]

According to the textbook we use, $$F$$ is a field over $$\Bbb{R}$$ or $$\Bbb{C}$$.

"A field over $\mathbb{R}$" sounds strange. There are vector spaces and algebras over fields. Perhaps $\mathbb{F}$ is simply a field.

I think for question one, we need to prove the existence of constants $${a}_{0},...,{a}_{m}$$ such that the linear functional $$\varphi (P) = {a}_{0}p(0) + \sum_{k=1}^{m} {p}^{(k)}(0)$$
Not really sure how to go from there

I think $p$ should be lowercase in the left-hand side as well.

Every functional on $\mathbb{F}^m$ has the form $\varphi((b_0,\ldots,b_m))=a_0b_0+\dots a_mb_m$ for some constants $a_0,\ldots,a_m$. Now suppose $p(t)=b_0+b_1x+\dots b_mx^m$. What are $p(0), p'(0), \ldots, p^{(m)}(0)$?

I'm a bit confused about the mapping, is it saying that when we have a polynomial P(z), the map makes it goes to p(0) for all z?

Yes, I believe the function maps a polynomial $p(z)$ to $(p(0))^2$. The question is whether it is a linear functional.

In problem 3, what is the third derivative of a polynomial whose degree is at most 2?

For problem 4, extend $v$ to a basis of the space $V$.