StephenD420
- 97
- 0
Hello all:
I have a quick question concerning a variation of a planetary gear train I am working on.
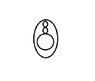
If I want a sun gear and then two planetary gears in between the sun and ring gear (like is shown in the attached picture), how do I find the number of teeth for the ring gear? Would the number of teeth still follow the formula R = 2P + S ?
Or would more gear teeth need to be added, and if so how many?
Example:
If the sun gear has say 94 teeth and the planetary gears have just 4 teeth would the ring gear have 102 teeth? or 104 teeth or some other number of teeth?
Thank you guys so much for the help.
Stephen
I have a quick question concerning a variation of a planetary gear train I am working on.
If I want a sun gear and then two planetary gears in between the sun and ring gear (like is shown in the attached picture), how do I find the number of teeth for the ring gear? Would the number of teeth still follow the formula R = 2P + S ?
Or would more gear teeth need to be added, and if so how many?
Example:
If the sun gear has say 94 teeth and the planetary gears have just 4 teeth would the ring gear have 102 teeth? or 104 teeth or some other number of teeth?
Thank you guys so much for the help.
Stephen