Oil Spill - Differential Equations

Click For Summary

Discussion Overview

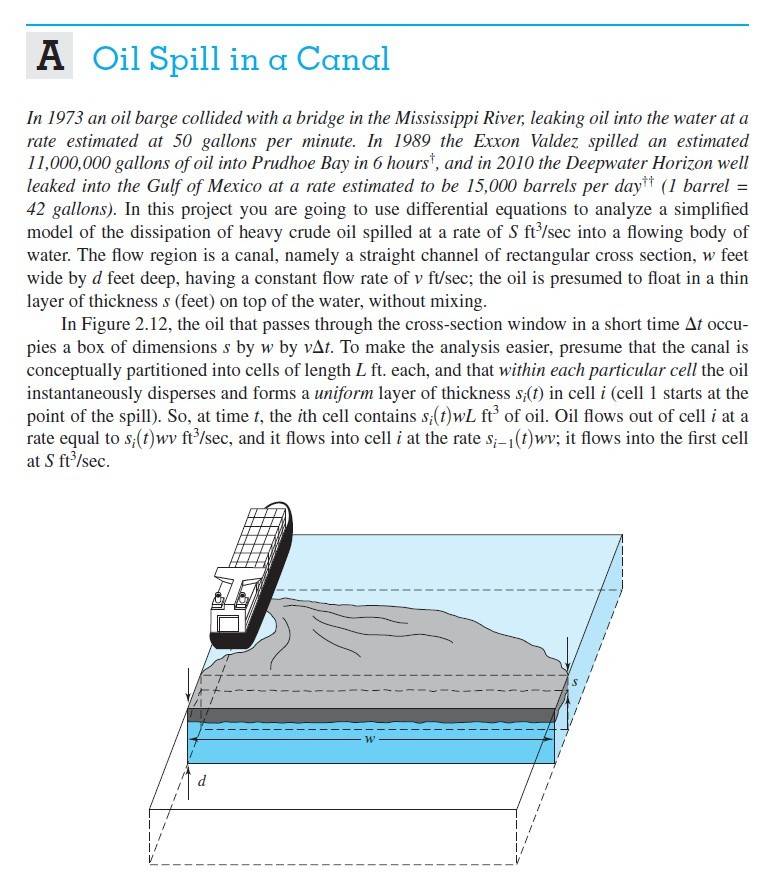
The discussion revolves around formulating and solving a differential equations (DE) problem related to oil spill dynamics. Participants explore various approaches to model the flow of oil between different cells over time, addressing both theoretical and practical aspects of the problem.

Discussion Character

  • Exploratory
  • Mathematical reasoning
  • Homework-related

Main Points Raised

  • One participant expresses difficulty in solving the DE problem and indicates a lack of understanding of the problem's requirements.
  • Another participant emphasizes the need for clarity on what has been attempted to provide effective assistance.
  • A participant outlines the flow dynamics, stating that the rate of oil flowing into a cell is equal to the rate flowing out of the previous cell, leading to a mathematical formulation involving derivatives.
  • The mathematical expression for the change in oil amount in a cell is presented, including a limit process that leads to a differential equation.

Areas of Agreement / Disagreement

Participants do not appear to reach a consensus on the understanding of the problem or the methods to solve it, indicating ongoing confusion and exploration of different approaches.

Contextual Notes

Participants have not fully articulated their assumptions or the specific conditions of the problem, and there are unresolved mathematical steps in the proposed formulations.

echianne
Messages
2
Reaction score
0
Hello everyone. I hope anyone can help me with this problem. I will greatly appreciate it. Willing to compensate anybody to answer this problem correctly for me.
277407932_705910683967009_541797176334639952_n.jpg
278675679_568002187886304_8047340021244904938_n.jpg
 
Physics news on Phys.org
echianne said:
Hello everyone. I hope anyone can help me with this problem. I will greatly appreciate it. Willing to compensate anybody to answer this problem correctly for me. View attachment 11832View attachment 11833
This is a free forum. We volunteer our time... payment is not necessary. However in order to help you best we need to have an idea of just where you are running into problems. What are you able to do with this?

-Dan
 
topsquark said:
This is a free forum. We volunteer our time... payment is not necessary. However in order to help you best we need to have an idea of just where you are running into problems. What are you able to do with this?

-Dan
Thank you so much. I have come up with different systems of DE but nothing seemed to work. I think there is something wrong with how I understood the problem.
 
echianne said:
Thank you so much. I have come up with different systems of DE but nothing seemed to work. I think there is something wrong with how I understood the problem.
What have you tried?

-Dan
 
The crucial information is in the last two sentences: "So at time t, the ith cell contains $s_i$ wL $ft^3$ of oil. Oil flows out of cell i at a rate equal to $s_i(t)$ wv $ft^3/s$ and flows into cell i at a rate equal to $s_{i-1}(t)$ wv $ft^3/s$. It flows into the first cell at rate S $ft^3/s$".

That is just saying that the rate oil flows into one cell is the rate at which it flows out of the previous cell.
The DERIVATIVE of the amount of oil ($s_i(t)$) at a given x (at a given cell) is the rate at which oil is flowing in minus the rate at which it is flowing out: $\Delta s_i(t)= (s_{i-1}(t)- s_i(t))\Delta t$.
$\frac{\Delta s_i(t)}{\Delata t}= (s_{i-1}(t)- s_i(t))= -(s_i(t)- s_{i-1})$.

Taking the limit as the length of each of each cell goes to 0, $\frac{ds}{dt}= s$ with initial value s(0)= S.
 

Similar threads

Undergrad Why Is a Differential Equation Called Nonlinear?
  • · Replies 3 ·
Replies
3
Views
3K
MHB How to prove that the Euler-Bernoulli equation is hyperbolic
  • · Replies 10 ·
Replies
10
Views
2K
Undergrad Solving Differential Equation Using Reduction of Order
  • · Replies 2 ·
Replies
2
Views
4K
Graduate Integrability of Systems of Differential Equations
  • · Replies 5 ·
Replies
5
Views
4K
Undergrad Is there a name for this sort of differential equation?
  • · Replies 2 ·
Replies
2
Views
2K
Graduate Is a solution of a differential equation a function of its parameters?
  • · Replies 3 ·
Replies
3
Views
2K
MHB Help with a question (Bernoulli General solution)
  • · Replies 8 ·
Replies
8
Views
2K
Undergrad Drawing Direction Fields for Higher Order ODEs
  • · Replies 6 ·
Replies
6
Views
3K
High School Basic Idea of Differential Equations
  • · Replies 25 ·
Replies
25
Views
3K
Undergrad Integral-form change of variable in differential equation
  • · Replies 1 ·
Replies
1
Views
2K