On charges in a bounded region which moves:

[elegysix]

So I asked my professor this question the other day, but I didn't get a clear answer. He said something about the fields being relative to each other, and so they didn't interact. Anyways, here is the setup:

Suppose we have a circular conducting plate of some radius, and on this plate there are two free charges with the same value of charge, (q₁=q₂). Where then, would the charges be? because the charges repel each other, it is a fair guess that they would be on the edge of the plate, where the distance between them is greatest. Suppose then, that the plate is moving with a constant velocity. Where would the charges be then?

My guess is that because each moving charge creates a magnetic field, the force of one charge's magnetic field on the other charge is q(VXB) which always points inward toward the axis the plate moves along. Perhaps a clearer explanation: As the plate moves along an axis, one charge lies along the leading edge of the plate, and the other along the trailing end of the plate, and a line between the two charges coincides with the axis the plate moves along. I've drawn a picture if it helps.

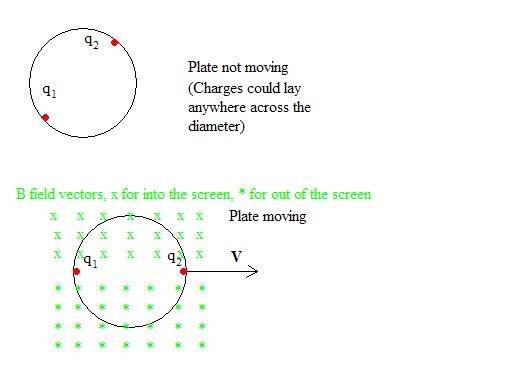
Is this correct? as I mentioned at first, I didn't get a clear answer from my professor. He said something about relative fields and them not interacting, but I couldn't follow what he was saying. Any thoughts?

 

[Meir Achuz]

1. You cannot keep charge on a conducting plate isolated as in your picture. Charge will spread out over the surface of the plate to keep the conductor as an equipotential.

2. If you calculate the surface charge distribution for the conductor at rest, the charge-current distribution on a moving conductor is most easily found by Lorentz transforming the rest frame charge distribution as part of a four-vector in special relativity. It is much more difficult to find the distributions working only in the moving frame.

Both of your pictures are wrong.

 

[elegysix]

I don't understand what you mean by "charge will spread out... to keep the conductor as an equipotential." I cannot think of how the surface could ever possibly be equipotential if there are discrete points of charge like an electron... or are you suggesting this is not the case, that I can't have discrete points of charge?

perhaps you wouldn't mind explaining a little more? I'm relatively new to lorentz transforms, special relativity, and have no idea how to calculate a surface charge distribution.

 

[Meir Achuz]

I cannot think of how the surface could ever possibly be equipotential if there are discrete points of charge like an electron... or are you suggesting this is not the case, that I can't have discrete points of charge?

You can't have discrete points of charge on a conductor.
Don't worry about Lorentz transformations yet. Try to understand conductors.
Finding the surface charge distribution on a conducting plate is a hard enough problem.
Wait until you learn more EM.

 

[elegysix]

Interesting concept. Well suppose we say it is not a conducting plate, but an insulator, in which the charges are bound to those two specific points, is that plausible? If so, then is it valid to say the magnetic field from one particle causes a force on the other and vice versa?

 

[Meir Achuz]

To some extent. The E and B fields of a moving charge requires special relativity.
That is why Einstein titled his paper "The electrodynamics of moving bodies".
Wait until you have a good course including relativity, before answering this.

 

[Bob S]

Clem is correct. The charges are everywhere at the same time** (the charge density is minimized). Let's not worry about the indivisibility of the electrons here. It is uesful to consider the conducting plate in an environment where all of the two charges' field lines terminate on negative charges someplace out of sight. The charge is probably half on each side of the plate.

**This because the plate is part of an electric circuit, and surrounded by empty space. The velocity of electrical signals in empty space is v = 1/sqrt(u₀e₀) = c, where u₀ and e₀ are the permeability and permittivity of empty space. So the charges distribute at the speed of light.

Bob S