mathmari
Gold Member
MHB
- 4,984
- 7
Hey! 
We consider the TSP in Grid-City.
The roads in Grid-City have the form of a grid, so that the intersection points can be described by an integer coordinate system.
The distance of $2$ points $C=(x,y)$ and $D=(x',y')$ is defined as $d(C,D)=|x-x'|+|y-y'|$.
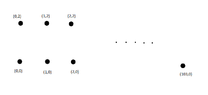
An input for the TSP consists of $203$ points with the following coordinates:
$$(i,0), \text{ for } i=0, 1, \dots , 100, \\ (i,2), \text{ for } i=0, 1, \dots , 100, \\ (103, 0)$$
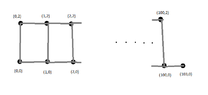
I want to give the optimal TSP-Tour. We have the following grid, or not?
View attachment 5787
(Wondering)
To find the optimal TSP-Tour from which point do we start? From which point we want? (Wondering)
If we choose one point to start, let's consider the $S=(0,0)$.
The second point will be either $A=(0,2)$ or $B=(1,0)$, right? Since $2=d(S,A)>d(S,B)=1$, the second point is $B=(1,0)$.
Or can we consider for the second point also the diagonal one, $(1,2)$ ? (Wondering)
Or is this not the correct way to find the optimal TSP-Tour? (Wondering)
When the roads are just the vertical and horizontal lines, we have that the distance of a point $(i,j)$ to an other is either $d_1=1$ or $d_2=2$, or not? (Wondering)
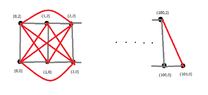
If this is true, is the optimal TSP-Tour the following?
$$(0,0)\rightarrow (1,0) \rightarrow (2,0) \rightarrow \dots \rightarrow (100,0)\rightarrow (103,0)\rightarrow (100,2) \rightarrow (99,2) \rightarrow \dots \rightarrow (1,2) \rightarrow (0,2) \rightarrow (0,0)$$
But how do we get from the point $(103,0)$ to the point $(100,2)$ ? (Wondering)
We consider the TSP in Grid-City.
The roads in Grid-City have the form of a grid, so that the intersection points can be described by an integer coordinate system.
The distance of $2$ points $C=(x,y)$ and $D=(x',y')$ is defined as $d(C,D)=|x-x'|+|y-y'|$.
An input for the TSP consists of $203$ points with the following coordinates:
$$(i,0), \text{ for } i=0, 1, \dots , 100, \\ (i,2), \text{ for } i=0, 1, \dots , 100, \\ (103, 0)$$
I want to give the optimal TSP-Tour. We have the following grid, or not?
View attachment 5787
(Wondering)
To find the optimal TSP-Tour from which point do we start? From which point we want? (Wondering)
If we choose one point to start, let's consider the $S=(0,0)$.
The second point will be either $A=(0,2)$ or $B=(1,0)$, right? Since $2=d(S,A)>d(S,B)=1$, the second point is $B=(1,0)$.
Or can we consider for the second point also the diagonal one, $(1,2)$ ? (Wondering)
Or is this not the correct way to find the optimal TSP-Tour? (Wondering)
When the roads are just the vertical and horizontal lines, we have that the distance of a point $(i,j)$ to an other is either $d_1=1$ or $d_2=2$, or not? (Wondering)
If this is true, is the optimal TSP-Tour the following?
$$(0,0)\rightarrow (1,0) \rightarrow (2,0) \rightarrow \dots \rightarrow (100,0)\rightarrow (103,0)\rightarrow (100,2) \rightarrow (99,2) \rightarrow \dots \rightarrow (1,2) \rightarrow (0,2) \rightarrow (0,0)$$
But how do we get from the point $(103,0)$ to the point $(100,2)$ ? (Wondering)
Attachments
Last edited by a moderator: