MHB Optimizing Seating Arrangements: Maximizing Capacity and Minimizing Tables

[MarkFL]

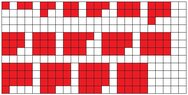
We wish to find how many people can be seated around a table. We may form larger tables by pushing together smaller square tables and arranging people as shown in the diagram:

View attachment 1261

There are two rules we are required to follow when pushing the smaller tables together and arranging the people around the larger table:

• Only 1 person may be seated at one side of a smaller table
• The larger table must be made as square as possible

Determine:

a) The number of people that may be seated for a given number of smaller tables.

b) The minimum number of smaller tables required to seat a given number of people.

 

[alyafey22]

The statement '' as square as possible '' is a little bit vague !

 

[MarkFL]

This is the "algorithm" I used for forming the larger tables:

View attachment 1264

While there are other ways to go about it to get the same results, to me this is the most straightforward way to approach the problem.

 

[eddybob123]

For a), it seems like there is no general formula for the number of people. If a table is placed in a "corner", the number of people stays the same. Otherwise, it increases by two. It's hard to tell where a table is going to be placed in advance.
b) only works if the number of people is even. But there also seems to be no formula.

 

[alyafey22]

It seems like a pattern on creating the tables , we start by ,say, a square then we add 1 square so it becomes a rectangle then we add two units it becomes a square then adding two units it becomes a rectangle adding now three units it becomes a square again and so on .

So Assume that We start by a square we add a number of units equal to its length that transfers it to a rectangle with a parameter in terms of the length of the square .

So nice structure .

Mark , what algorithm did you use ?

 

[MarkFL]

...
Mark , what algorithm did you use ?

I will be posting my solutions soon, but I want to give everyone a chance first...(Tongueout)

 

[I like Serena]

If the complete table is square with side k, you have 4k seats.

With fewer tables this does not change, until you get a rectangle of k x (k-1) tables.
Then you get 2 places fewer.

With 1 table more than k x k, you get 2 extra places, which again doesn't change until you have k x (k+1) tables.

Therefore:
$$\text{seats}(n)=\begin{cases}
4k & \text{if }\exists k \text{ such that } k(k-1) < n \le k^2 \\
4k + 2 & \text{if }\exists k \text{ such that } k^2 < n \le k(k+1)
\end{cases}$$

I'll put a more beautiful formula in a later post, but I have to sleep first. (Sleepy)

 

[MarkFL]

Here is my solution:

Spoiler

If $T$ is the number of tables and $p$ is the number of people seated, then:

$$p=2\left\lceil\,\frac{\lceil 4\sqrt{T}\rceil}{2}\,\right\rceil$$

To find the minimum number of tables to seat $p$ people, use:

$$T_{\min}=\left\lceil \left(\frac{p}{4} \right)^2-\frac{p}{4}+1 \right\rceil$$

I began with the basis $$p=4\sqrt{T}$$.

I then noticed this needed to be rounded up to the next even number. So I used the ceiling function to round the basis up to the the next greatest integer, then used the ceiling function again to round that result up to the next even integer.

As for the the minimum number of tables needed, I observed that when $T$ is a perfect square, we could subtract 1 less than the square root of $T$ and still seat the same number of people.