Outer Measure .... Axler, Result 2.5 ....

[Math Amateur]

I am reading Sheldon Axler's book: Measure, Integration & Real Analysis ... and I am focused on Chapter 1: Measures ...

I need help with the proof of Result 2.5 ...

Result 2.5 and its proof read as follows:

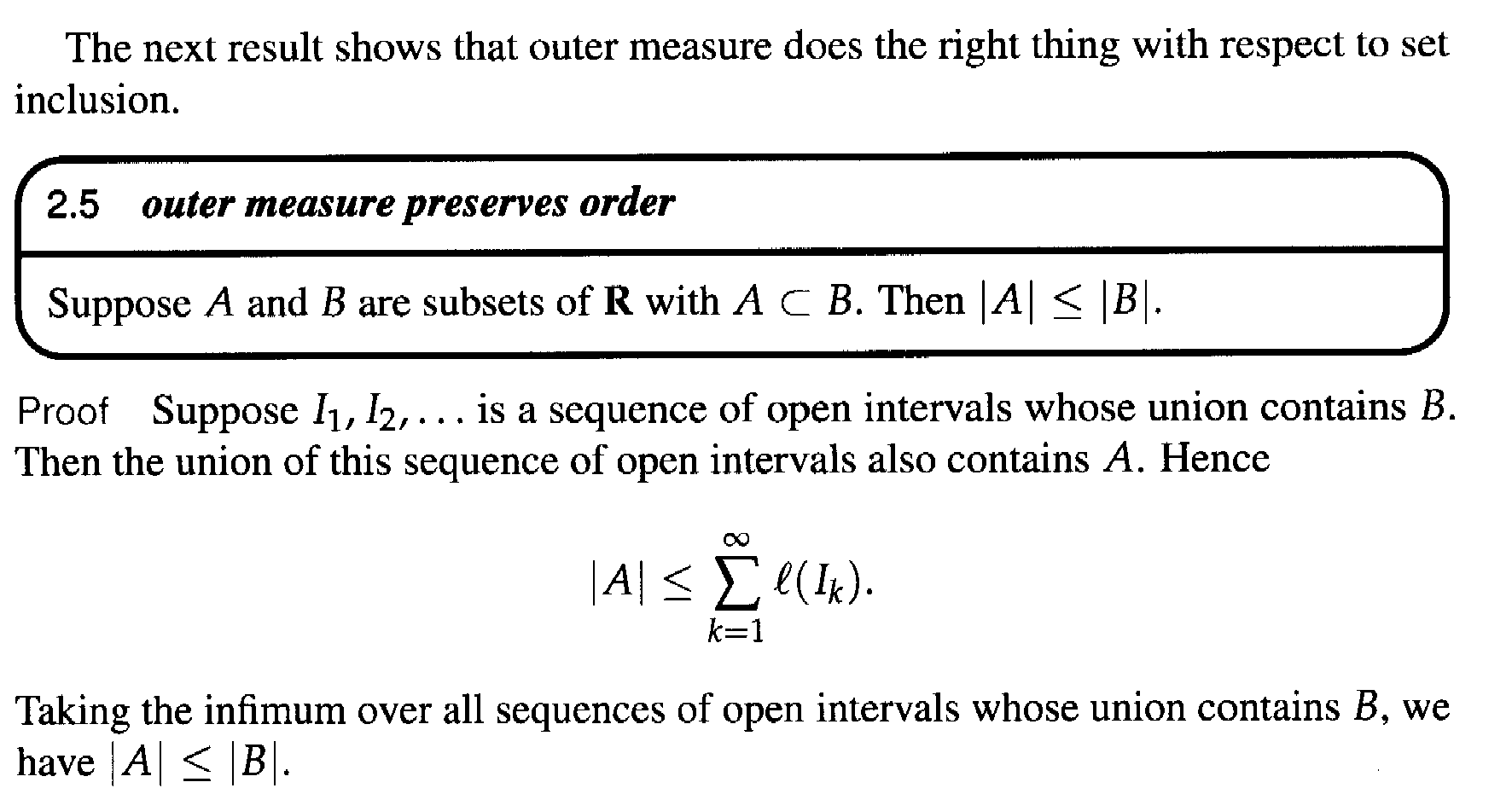
Now $$ \mid A \mid \leq \sum_{ k = 1 }^{ \infty } l(I_k)$$ follows from Axler's definition of outer measure ( is that correct?) ... see definition below ...

Then essentially we have to prove that $$ \mid A \mid \leq \sum_{ k = 1 }^{ \infty } l(I_k) \Longrightarrow \mid A \mid \leq \text{ inf } ( \sum_{ k = 1 }^{ \infty } l(I_k) \text{ where } B \subset \cup_{ k = 1 }^{ \infty } I_k ) $$ ...

But how do we rigorously prove this ...

Can someone please demonstrate a formal and rigorous proof that:

$$\mid A \mid \leq \sum_{ k = 1 }^{ \infty } l(I_k) \Longrightarrow \mid A \mid \leq \text{ inf } ( \sum_{ k = 1 }^{ \infty } l(I_k) \text{ where } B \subset \cup_{ k = 1 }^{ \infty } I_k ) $$ ...Help will be much appreciated ...===============================================My thoughts ...

Perhaps we can assume that $$\mid A \mid \ \gt \text{ inf } ( \sum_{ k = 1 }^{ \infty } l(I_k) \text{ where } B \subset \cup_{ k = 1 }^{ \infty } I_k ) $$ ... and obtain a contradiction ...

We have that $$ \mid A \mid \ \gt \text{ inf } ( \sum_{ k = 1 }^{ \infty } l(I_k) \text{ where } B \subset \cup_{ k = 1 }^{ \infty } I_k ) \Longrightarrow \ \exists \ \sum_{ k = 1 }^{ \infty } l(I_k)$$ such that $$\mid A \mid \ \gt \sum_{ k = 1 }^{ \infty } l(I_k)$$ where $$\sum_{ k = 1 }^{ \infty } I_k$$ covers $$B$$ ... Is this a contradiction ...? why exactly? How would you explain the contradiction clearly and rigorously ...

Hope that someone can help ...

Peter=============================================================================================================

Readers of the above post may be assisted by access to Axler's definition of the length of an open interval and his definition of outer measure ... so I am providing access to the relevant text ... as follows:

Hope that helps ...

Peter

 

[GJA]

Hi Peter,

You're almost there. Note that the collection of intervals is also a cover of $A$. Can you arrive at your contradiction using this fact?

 

[Math Amateur]

Hi Peter,

You're almost there. Note that the collection of intervals is also a cover of $A$. Can you arrive at your contradiction using this fact?

Thanks for the help GJA ...

I think I can proceed now ... as follows ...

Assume that $$\mid A \mid \ \gt \text{ inf } ( \sum_{ k = 1 }^{ \infty } l(I_k) \text{ where } B \subset \cup_{ k = 1 }^{ \infty } I_k ) $$

... then $$\ \exists \ $$ a particular covering $$I_1, I_2, I_3,$$ ... of $$B$$ such that $$\mid A \mid \ \gt \sum_{ k = 1 }^{ \infty } l(I_k)$$ where $$B \subset \cup_{ k = 1 }^{ \infty } I_k $$

But this particular covering also covers $$A$$ since $$A \subset B$$ ...

... so that $$\mid A \mid \ \leq \sum_{ k = 1 }^{ \infty } l(I_k)$$ ... since $$\mid A \mid$$ is a lower bound on $$\sum_{ k = 1 }^{ \infty } l(I_k)$$ for all coverings $$I_1, I_2, I_3,$$ ... of $$A$$

... BUT ... $$\mid A \mid \ \leq \sum_{ k = 1 }^{ \infty } l(I_k)$$ is a contradiction of our assumption ...
Is the above correct?

Can someone please critique the above argument ...

Help will be appreciated ...

Peter

 

[GJA]

Looks great, Peter. Nicely done!

 

[Math Amateur]

Thanks GJA ... appreciate your help as usual...

Peter