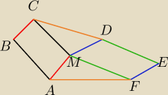
MHB Can Parallelograms Be Constructed in a Convex Hexagon?
- Thread starter maxkor
- Start date
-
- Tags
- Hexagon
Click For Summary
SUMMARY
In a convex hexagon $ABCDEF$, if there exists a point $M$ such that $ABCM$ and $DEFM$ are parallelograms, then it can be conclusively proven that there exists another point $N$ such that $BCDN$ and $EFAN$ are also parallelograms. This conclusion relies on the properties of parallelograms and the geometric relationships within the hexagon. The proof utilizes vector addition and the properties of midpoints to establish the existence of point $N$.
PREREQUISITES- Understanding of basic geometric properties of parallelograms
- Familiarity with convex polygons, specifically hexagons
- Knowledge of vector addition and geometric proofs
- Ability to visualize geometric configurations and relationships
- Study the properties of parallelograms in polygonal geometry
- Explore vector geometry and its applications in proving geometric theorems
- Learn about the characteristics of convex polygons and their implications
- Investigate advanced geometric proofs involving multiple points and shapes
Mathematicians, geometry enthusiasts, educators teaching geometric concepts, and students preparing for advanced mathematics competitions.
Similar threads
- · Replies 1 ·
- · Replies 9 ·
- · Replies 9 ·
- · Replies 5 ·
- · Replies 1 ·
High School
Counting intersections of lines in a triangle
- · Replies 30 ·
- · Replies 8 ·