Pg345's question at Yahoo Answers regarding motion with uniform acceleration

[MarkFL]

Here is the question:

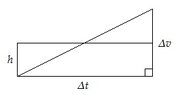
Uniformly Accelerating Motion?

Consider an object that accelerates uniformly. If you were to calculate the average speed of the object for a given interval of time, would the object ever be traveling with an instantaneous speed equal to that average speed? If so when? Explain!

I have posted a link there to this topic so the OP can see my work.

 

[MarkFL]

Re: pg345's question at Yahoo! Answers regading motion with uniform acceleration

Hello pg345,

Let's denote the acceleration of the object as $a$, and use the fact that acceleration is defined as the time rate of change of velocity to write:

\(\displaystyle \frac{dv}{dt}=a\) where \(\displaystyle v(0)=v_0\)

Separating variables and integrating, we find:

\(\displaystyle \int_{v_0}^{v(t)}\,du=a\int_0^t\,dw\)

\(\displaystyle v(t)-v_0=at\)

\(\displaystyle v(t)=at+v_0\)

Now, to find the average velocity on some interval $t_1\le t\le t_2$, we may use:

\(\displaystyle \overline{v(t)}=\frac{1}{t_2-t_1}\int_{t_1}^{t_2}at+v_0\,dt\)

\(\displaystyle \overline{v(t)}=\frac{1}{t_2-t_1}\left[\frac{a}{2}t^2+v_0t \right]_{t_1}^{t_2}\)

\(\displaystyle \overline{v(t)}=\frac{1}{t_2-t_1}\left(\frac{a}{2}t_2^2+v_0t_2-\frac{a}{2}t_1^2-v_0t_1 \right)\)

\(\displaystyle \overline{v(t)}=\frac{1}{t_2-t_1}\left(\frac{a}{2}\left(t_2+t_1 \right)\left(t_2-t_1 \right)+v_0\left(t_2-t_1 \right) \right)\)

\(\displaystyle \overline{v(t)}=a\left(\frac{t_2+t_1}{2} \right)+v_0\)

\(\displaystyle \overline{v(t)}=v\left(\frac{t_1+t_2}{2} \right)\)

So, we see that we will always have the instantaneous velocity equal to the average velocity at the midpoint of the interval.

Perhaps this can be more easily seen geometrically. Consider the following diagram:

View attachment 1280

We have a right triangle if base $\Delta t$ and altitude $\Delta v$. Its area represents the distance traveled during the time interval $\Delta t$, given the linear velocity function that results from uniform acceleration. Now, we wish to find some value of $h$ such that the rectangle whose base is $\Delta t$ and whose height is $h$, which corresponds to the average velocity, has an area equal to the triangle. Hence:

\(\displaystyle \frac{1}{2}\Delta t\Delta v=\Delta th\)

Divide through by $\Delta t$ and arrange as:

\(\displaystyle h=\frac{1}{2}\Delta v\)

Let \(\displaystyle h=\overline{v(t)}\):

\(\displaystyle \overline{v(t)}=\frac{1}{2}\Delta v=a\frac{\Delta t}{2}=a\frac{t_2-t_1}{2}\)

And so to find the time for which this is true, we may write:

\(\displaystyle t-t_1=\frac{t_2-t_1}{2}\)

\(\displaystyle t=\frac{t_2-t_1}{2}+t_1=\frac{t_1+t_2}{2}\)