- 22,170
- 3,327
What will happen to the balance:
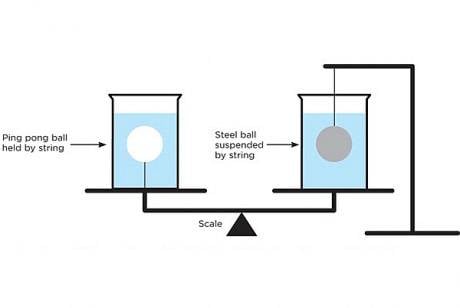
The forum discussion centers around a physics riddle involving buoyancy and balance scales with two different balls: a steel ball and a ping pong ball. Participants conclude that the scale will tilt towards the ping pong ball due to the upward buoyant force acting on it, which counterbalances its weight and the string attached to it. The discussion highlights the importance of understanding buoyancy, as both balls displace the same volume of water, yet the forces acting on them differ based on their respective weights and the air inside the ping pong ball.
PREREQUISITESPhysics students, educators, and anyone interested in understanding buoyancy and its implications in real-world scenarios, particularly in experimental physics.
 )
)micromass said:What will happen
D H said:Way to go Zeta!
There apparently are a lot of people here who think they can pick themselves up by their bootstraps.
BobKat said:It boils down to this question: Does the upward force caused by the air inside the ping pong ball counterbalance the added weight of the ping pong ball itself and the string which holds it. Both balls displace the same amount of water (presumably) and the ball on the right adds no weight to the right side. I suspect the scale stays even, because the air lifts the ball and string - BUT the string is attached to the bottom of the glass, so I don't think it can lift the glass by its own bootstrap (string).
BobKat said:Guess I don't understand how the steel ball contributes the weight of its volume in water to the weight on the right...
BobKat said:Guess I don't understand how the steel ball contributes the weight of its volume in water to the weight on the right...
"easiest to think of it..."? I did not understand one word of what you said. And their weights (including the balls in them) are not the same.chingel said:I think it is easiest to think of it in terms of external forces on the containers, since their weights are the same. The pressure of the water depends only the the height of the water level, which is the same for both of them, but the left container has an additional string pulling it up.
I think we have to be careful not to say that the steel ball's weight somehow channels through the water, because the water pressure is the same in both containers.
Gerinski said:"easiest to think of it..."? I did not understand one word of what you said. And their weights (including the balls in them) are not the same.
The buoyant force on each ball is the same. Buoyant force depends only on the volume of fluid displaced, not the mass of the ball itself.derek10 said:I still don't get it:
Why does the steel ball have buoyancy and the ping pong one doesn't? is it because the steel one is more massive than the other?
(BTW I though than the balance would lean to the left due to the extra weight of the ping pong ball)
Doc Al said:The buoyant force on each ball is the same. Buoyant force depends only on the volume of fluid displaced, not the mass of the ball itself.
Extra weight of the ping pong ball?
That was my first idea too. And it seems like the simplest argument so far to me.chingel said:Water pressure on both of the containers is exactly the same everywhere, but the left container has an extra string attached to it pulling it up, therefore it will go up.
You have two identical steel balls hanging on opposite sides of a scale like this:

You have two buckets, one with water and one with glycerin, standing on opposite sides of a scale like this:
Both scales are initially balanced. Then you fully submerge the balls into the buckets without touching the walls.
Does the balance of the scales change? If yes, how?
A.T. said:Here is a similar one:
I don't thing that's correct, the string in the left container is not pulling it up, as someone said "nobody can lift himself by pulling his bootstraps".chingel said:View the container itself as a system, viewing everything inside and outside of it as external. The containers themselves are the same, they weigh the same. Water pressure on both of the containers is exactly the same everywhere, but the left container has an extra string attached to it pulling it up, therefore it will go up.