Piece-wise linear diode model

[dalarev]

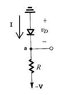
I am NOT trying to solve this as a homework problem, I'm just trying to dig out basic concepts that I'm missing when using this battery+resistance diode model.


I'm having trouble seeing why, when solving for current, KCL equation does NOT work out as:

1) I= (0-Va)/rd
2) I=(Va-(-5))/R

where Va is the voltage at node a, rd is the diode resistance, and Vd0 is the diode voltage drop.

I understand that the resistors are in series, and there is only one current, so the correct Kirchoff's equation should be:

I=(0-Vd0)/(rd+R)

But each resistor is responsible for a (different) voltage drop. The position of the resistors, even if they are in series, is specific. We can see this by measuring voltages before and after a resistor. Hopefully somebody can provide a fullproof explanation for this.

 

[dalarev]

Here's an example directly from the book which very clearly shows the question that I have:

They give us the equation for the current, since there is only one current, and the resistors are in series.

My question is, why is the equation for I NOT:

1) I=(Vdd-Vd0)/R
2) I=(Vd0-0)/rd

Each resistor is responsible for a voltage drop, meaning that it is important where each resistor is located. Where am I going wrong?

 

[Redbelly98]

V_DD - V_D0 gives the sum of the voltage drops across R and r_D, hence the given equation for I.

1) I=(Vdd-Vd0)/R

No, because (Vdd-Vd0) is not the voltage across R.

2) I=(Vd0-0)/rd

No, because Vd0 is not the voltage drop across r_D

 

[dalarev]

No, because (Vdd-Vd0) is not the voltage across R.

Why not? I'm just following from one voltage source to another, isn't that how KCL works?

 

[Redbelly98]

It's KVL that we want to use here ... KCL just tells us that the current is the same through each element in the loop.

According to KVL:

V_DD - I_D*R - V_D0 - I_D*r_D = 0​

You can rearrange that to get

V_DD - V_D0 = I_D*R + I_D*r_D​

Note the right-hand-side has the voltages across both resistors.

 

[dalarev]

Thanks for that, made me realize something I didn't recall:

Consider the entire voltage across the diode, first; then, KVL becomes:

I=(-vd-(-5))/R

from node a to Vss. Now, realizing that for this diode model, the voltage across the diode, (variable) vd:

vd=Vd0+I*rd

where Vd0 is the intrinsic threshold voltage (constant).

Substituting in the original equation for I and playing around with some algebra leads us to:

I=(-Vd0+5)/(R+rd)

which I'm hoping is the right answer. Thanks for the refresher.

 

[Redbelly98]

Looks good, assuming -V = -5V in your first circuit.