Master1022
- 590
- 116
- Homework Statement
- Find the value of the collapsed load factor when Mp = 120 kN/m
- Relevant Equations
- Plastic energy dissipated = work done by loads
Hi,
I have a quick question about part 1 of this upper bound theorem question (in the attached image). Answer says that \lambda_c = 2.25.
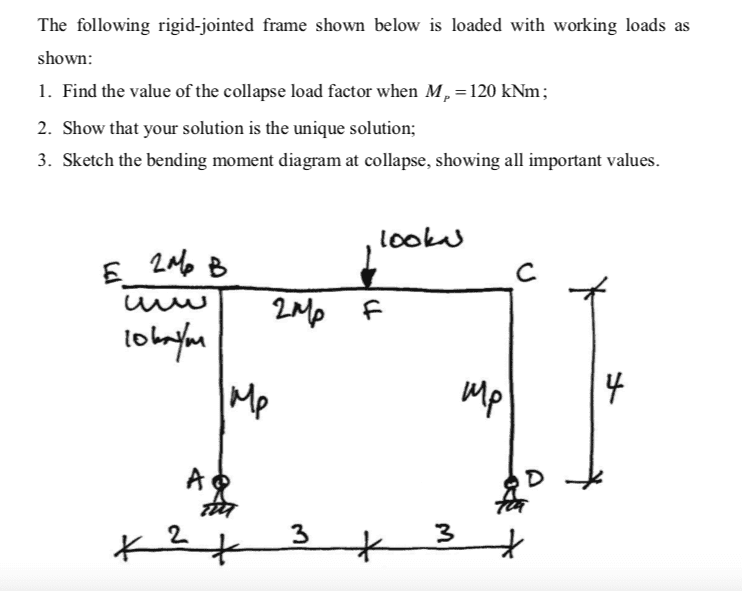
First, we know that there is 1 redundancy and therefore there will be a maximum of 2 plastic hinges for failure.
I have found that there needs to be swaying to right of the right side of the structure (by an angle \theta), but I don't have any intuition for why that would be the case. Would someone be able to explain to me why there must be swaying in the structure for the mechanism illustrated? If I update my answer below to include this, then I get the correct answer.
(Initial drawing without the swaying)
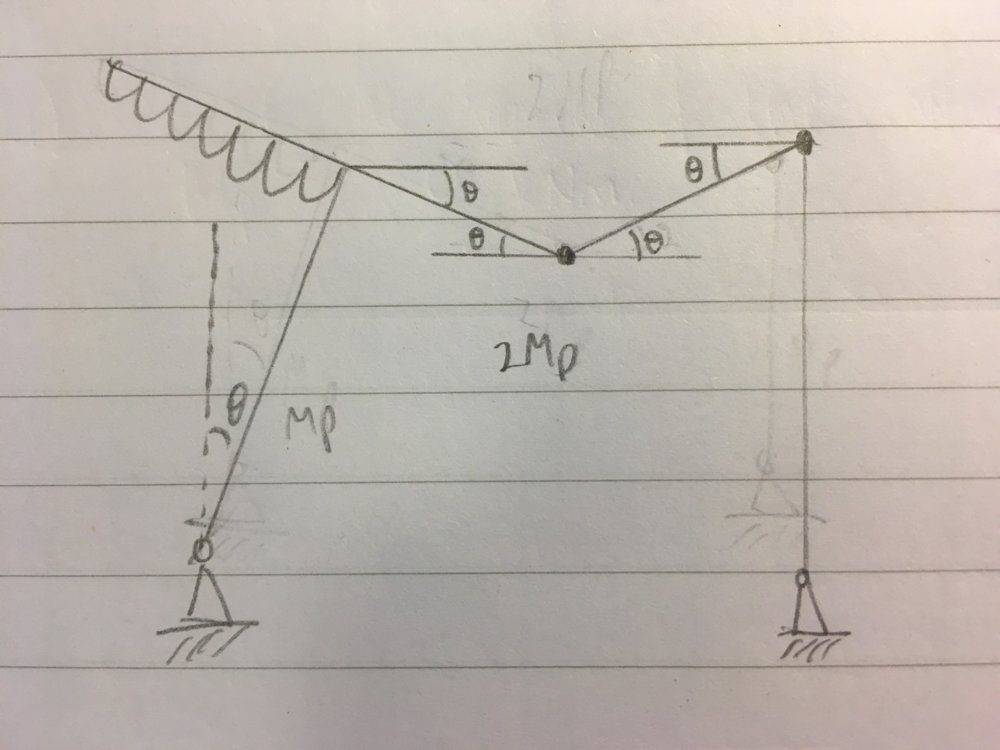
Doing my original incorrect analysis yields:
M_p \left( \theta \right) + 2 M_p \left( 2 \theta \right) = 100 \lambda \left( 3 \theta \right) + w \lambda \left( \frac{1}{2} 2 \left( 2 \theta \right) \right)
Substituting in the values from the question, that will yield \lambda = \frac{600}{320} = 1.875, which isn't the correct answer.
I have a quick question about part 1 of this upper bound theorem question (in the attached image). Answer says that \lambda_c = 2.25.
First, we know that there is 1 redundancy and therefore there will be a maximum of 2 plastic hinges for failure.
I have found that there needs to be swaying to right of the right side of the structure (by an angle \theta), but I don't have any intuition for why that would be the case. Would someone be able to explain to me why there must be swaying in the structure for the mechanism illustrated? If I update my answer below to include this, then I get the correct answer.
(Initial drawing without the swaying)
Doing my original incorrect analysis yields:
M_p \left( \theta \right) + 2 M_p \left( 2 \theta \right) = 100 \lambda \left( 3 \theta \right) + w \lambda \left( \frac{1}{2} 2 \left( 2 \theta \right) \right)
Substituting in the values from the question, that will yield \lambda = \frac{600}{320} = 1.875, which isn't the correct answer.
Attachments
Last edited:
