Please explain the proofs for sin(90 - θ)

[jayanthd]

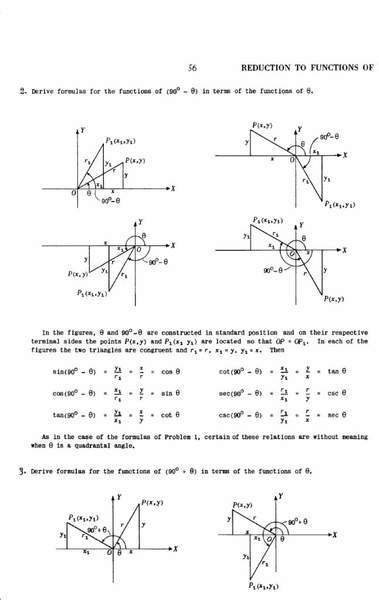
Please see the attached image. There are 6 figures.

Please explain the proofs for sin(90 - θ) w.r.t the 2nd, 3rd and 4th images. I understand the proof w.r.t 1st image.

In the 2nd image y1 and x is negative. In 3rd image y, y1, x, x1 are all negative and in the 4th image y and x1 are negative. How he gets +ve value for sin(90 - θ) w.r.t 2nd, 3rd and 4th figures?

In the 3rd fig. -y1 = -x and -y = -x1.

-y1/r1 = -x/r = -cos(θ)

 

[HallsofIvy]

I don't understand your question. If, as in #2, the top figure on the right, 90< \theta< 180, sin(90- \theta) is certainly negative. Where does he say that it is positive?

 

[jayanthd]

He is proving with the top four figures that sin(90 - θ ) = cos(θ). It is from the book "Theory and Problems of Plane and Spherical Trigonometry by Frank Ayres, Schaum's Outline Series"

The book is available here. http://archive.org/details/SchaumsTheoryProblemsOfTrigonometry

Please explain the proofs in page nos 56 and 57.

In the 2nd figure from top ∠AOP = (180 - θ). How does he say ∠BOP1 = (90 - θ)?

and ∠OAP and ∠OBP1 = 90.