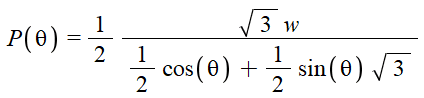SUMMARY
The discussion focuses on solving for the minimum value of P, denoted as P(theta)min, specifically identifying that the minimum occurs at ##\sqrt{3}/2##. The solution involves recognizing the expression as a combination of sine and cosine functions, leading to the conclusion that the maximum of the sine function is 1, which corresponds to ##\theta = \pi/3##. The method discussed includes using double-angle formulas and the combination of sine waves to derive the minimum value effectively.
PREREQUISITES
- Understanding of trigonometric identities, specifically sine and cosine functions.
- Familiarity with the concept of maxima and minima in calculus.
- Knowledge of double-angle formulas in trigonometry.
- Ability to manipulate and combine trigonometric functions.
NEXT STEPS
- Study the application of double-angle formulas in trigonometric equations.
- Learn about the properties of sine and cosine functions, particularly their maxima and minima.
- Explore the concept of combining sine and cosine functions using quadrature.
- Investigate differentiation techniques for finding extrema in calculus.
USEFUL FOR
Mathematicians, physics students, and anyone interested in solving trigonometric optimization problems will benefit from this discussion.
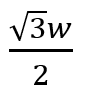 ?
?