Position of elevator given velocity vs time

[drjohn15]

Homework Statement

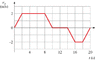
You are consulting for an elevator company. During a safety test, technicians created the following graph of the velocity of the elevator versus time; you have been asked to interpret the graph. Unfortunately, you are told that the technician who printed the graph has made two mistakes. The labeled interval on the velocity axis should be 2.1 m/s rather than 2.0 m/s, and the labeled time interval should be 4.2 s rather than 4.0 s. You should begin by redrawing the graph on your own paper with the proper labels on the velocity and time axes.

Since this motion is purely one-dimensional, give your answers to the following questions using a coordinate system consisting of a y-axis in the Up-Down direction with Up as positive. Indicate directions by the appropriate plus or minus sign. Assume that the test begins (at time zero) with the elevator at position y0=-3.1 m (i.e. 3.1 meters below ground level -- ground level has been selected as the location at which y=0).

Homework Equations

Velocity vs Time:

$t = 0\ s$, $v = 0\ m/s$
$t = 2.1\ s$, $v = 2.1\ m/s$
$t = 4.2\ s$, $v = 2.1\ m/s$
$t = 6.3\ s$, $v = 2.1\ m/s$
$t = 8.4\ s$, $v = 2.1\ m/s$
$t = 10.5\ s$, $v = 0\ m/s$
$t = 12.6\ s$, $v = 0\ m/s$
$t = 14.7\ s$, $v = 0\ m/s$
$t = 16.8\ s$, $v = -2.1\ m/s$
$t = 18.9\ s$, $v = -2.1\ m/s$
$t = 21\ s$, $v = 0\ m/s$

$v = Δy/Δt$ (y is the variable in this case)

The Attempt at a Solution

What is the position of the elevator at time 2.1 seconds? ... 8.4 seconds? ... etc.

$v = 2.1\ m/s = \frac{y_f - (-3.1\ m)}{2.1\ s - 0\ s}$

$\Delta y = 4.41\ m = y_f + 3.1\ m$

$y_f = 1.31\ m$

This answer is incorrect and I'm not sure where I'm going wrong with this. I even tried to enter
$1.3\ m$ and that was incorrect as well.

Any help would be greatly appreciated.

 

[tiny-tim]

welcome to pf!

hi drjohn15! welcome to pf!

What is the position of the elevator at time 2.1 seconds? ... 8.4 seconds? ... etc.

$v = 2.1\ m/s = \frac{y_f - (-3.1\ m)}{2.1\ s - 0\ s}$

$\Delta y = 4.41\ m = y_f + 3.1\ m$

$y_f = 1.31\ m$

This answer is incorrect and I'm not sure where I'm going wrong with this. I even tried to enter
$1.3\ m$ and that was incorrect as well.

(why are your time increments 2.1 and not 4.2 ? )

it's difficult to tell without seeing the graph,

but i'll guess that the experiment started with he lift stationary for 2.1s, so that y_2.1 is still 0

 

[haruspex]

i'll guess that the experiment started with he lift stationary for 2.1s, so that y_2.1 is still 0

I'll make a different guess - that the graph shows a straight line from (0, 0) to (2, 4) (or whatever). If so, it underwent uniform acceleration for that time period.

$v = 2.1\ m/s = \frac{y_f - (-3.1\ m)}{2.1\ s - 0\ s}$

That formula would be right if 2.1 m/s were the average velocity for the first 2.1 s, but you are given it as the instantaneous velocity at the end of the first time period. If its speed increased uniformly from rest over that time, what was its average speed?

 

[drjohn15]

Thanks very much for the replies!

I've attached the given graph (didn't know how before).

 

[drjohn15]

That formula would be right if 2.1 m/s were the average velocity for the first 2.1 s, but you are given it as the instantaneous velocity at the end of the first time period. If its speed increased uniformly from rest over that time, what was its average speed?

From the lecture, the average speed is: $$average\ speed = \frac{d}{\Delta t}$$ where $d$ is distance traveled, and $\Delta t$ is the time elapsed. So how would I find the distance traveled?

From the data that I've been given and the data that I've calculated previously, I'm a little lost as to where to go from here...

$velocity\ @\ t = 2.1\ s \rightarrow 2.1\ m/s$
$\Delta t = 2.1\ s$
$y_0 = -3.1\ m$

 

[tiny-tim]

have you been taught about distance = area under the velocity graph?

(if not, forget i said it)

 

[Penguin'15]

Well I am a beginning physics student, so the following may not be correct.
Since this is a velocity versus time graph, the slope is going to give you acceleration. That means you know initial velocity, final velocity, time, and acceleration. If I were solving this, I would plug that information into one of these equations:
x=x0+v0t+(1/2)at2
v2=v20+2aΔx
x=x0+0.5(v0+vf)t

Hopefully this helps in some way...

 

[Penguin'15]

Sorry about the formulas...I'm still working on the latex thing.

 

[drjohn15]

have you been taught about distance = area under the velocity graph?

(if not, forget i said it)

This is it!

$position\ @\ t = 2.1\ s \rightarrow -3.1\ m + \frac{2.1\ s * 2.1\ m/s}{2} = -0.895\ m$
$position\ @\ t = 8.4\ s \rightarrow -0.895\ m + 6.3\ s * 2.1\ s = 12.335\ m$
$...etc.$

Thanks again!

 

[haruspex]

From the lecture, the average speed is: $$average\ speed = \frac{d}{\Delta t}$$ where $d$ is distance traveled, and $\Delta t$ is the time elapsed.

Quite so, and that is always valid.
As I guessed, the graph shows uniform acceleration from t=0 to t=2.1 (i.e. a straight line on the velocity-time graph). It follows that the average speed v_avg is the average of the initial and final speeds, (0+2.1)/2 = 1.05m/s. So you can use these two equations to find the distance traveled: d = v_avg*Δt = 1.05*2.1. Note that taking the average of the initial and final speeds is only valid for constant acceleration. You should also be able to see how this relates to areas on the graph.