nightshade123
- 82
- 0
[SOLVED] potential energy and turning points
A block slides on the frictionless loop the lopp track shown in this img, what is the min height at which it can start from rest and still make it around the loop
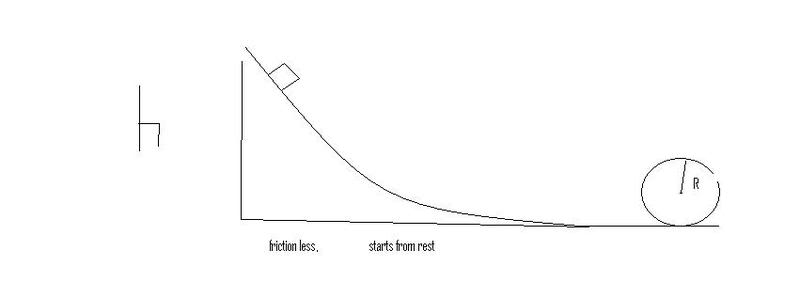
I haev solved this problem TWO ways, and i can't decide which way is correct
the eqn...
U0+K0 = K+U
where U = potential energy and K = kinetic energy
first
m * g * h + (1/2) * m * v^2 >= m * g * 2 * R
final answer = h = 2R
the other way is
m * g * h >= (1/2) * m * v^2 + m * g * 2 * R
final answer is h = (5*R) / 2??
Homework Statement
A block slides on the frictionless loop the lopp track shown in this img, what is the min height at which it can start from rest and still make it around the loop
The Attempt at a Solution
I haev solved this problem TWO ways, and i can't decide which way is correct
the eqn...
U0+K0 = K+U
where U = potential energy and K = kinetic energy
first
m * g * h + (1/2) * m * v^2 >= m * g * 2 * R
final answer = h = 2R
the other way is
m * g * h >= (1/2) * m * v^2 + m * g * 2 * R
final answer is h = (5*R) / 2??
Last edited: